Question

某厂生产的A产品按每盒10件进行包装，每盒产品均需检验合格后方可出厂．质检办法规定：从每盒10件A产品中任抽4件进行检验，若次品数不超过1件，就认为该盒产品合格；否则，就认为该盒产品不合格．已知某盒A产品中有2件次品．
（1）求该盒产品被检验合格的概率；
（2）若对该盒产品分别进行两次检验，求两次检验得出的结果不一致的概率．

Answer 1

【答案】分析：（1）若要求该盒产品被检验合格的概率，我们要先计算出该盒10件产品中任抽4件，有等可能的结果总数，然后再计算次品数不不超过1件（0件和1件两种情况）的事件数，然后代入公式即可得到结果．
（2）若对该盒产品分别进行两次检验，求两次检验得出的结果不一致，则有两种情况，一是第一次合格，第二次不合格，二是第一次不合格，第二次合格，代入公式即可得到结果．
解答：解：（1）从该盒10件产品中任抽4件，有等可能的结果数为C₁₀⁴种，
其中次品数不超过1件有C₈⁴+C₈³C₂¹种，
被检验认为是合格的概率为=．
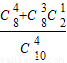
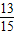
（2）两次检验是相互独立的，可视为独立重复试验，
因两次检验得出该盒产品合格的概率均为，
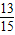
故“两次检验得出的结果不一致”
即两次检验中恰有一次是合格的概率为=．
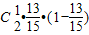
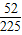
答：该盒产品被检验认为是合格的概率为；
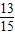
两次检验得出的结果不一致的概率为．
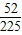
点评：本小题主要考查相互独立事件概率的计算，运用数学知识解决问题的能力，要想计算一个事件的概率，首先我们要分析这个事件是分类的（分几类）还是分步的（分几步），然后再利用加法原理和乘法原理进行求解．解决等可能性事件的概率问题，关键是要弄清一次试验的意义以及每个基本事件的含义是解决问题的前提，正确把握各个事件的相互关系是解决问题的关键．古典概型要求所有结果出现的可能性都相等，强调所有结果中每一结果出现的概率都相同．
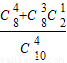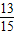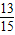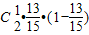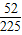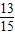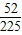