Question

4．如图，O为△ABC所在平面内一点，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，
（1）若△ABC的重心为G，试用$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$来表示$\overrightarrow{OG}$；
（2）若AD是△ABC的∠A的内角平分线，且$\frac{|\overrightarrow{AB}|}{|\overrightarrow{AC}|}$=λ，试用$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$来表示$\overrightarrow{AD}$．

Answer 1

分析 （1）作图，$\overrightarrow{OG}$=$\overrightarrow{OA}$+$\overrightarrow{AG}$=$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{AM}$=$\overrightarrow{a}$+$\frac{2}{3}$•$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）=$\overrightarrow{a}$+$\frac{1}{3}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），而$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{c}$-$\overrightarrow{a}$；从而解得；
（2）作图，设$\overrightarrow{AD}$=x（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$），从而表示出$\overrightarrow{CD}$=（$\frac{x}{|\overrightarrow{AC}|}$-1）$\overrightarrow{AC}$+$\frac{x}{|\overrightarrow{AB}|}$$\overrightarrow{AB}$；$\overrightarrow{BD}$=$\frac{x}{|\overrightarrow{AC}|}$$\overrightarrow{AC}$+（$\frac{x}{|\overrightarrow{AB}|}$-1）$\overrightarrow{AB}$；
由共线可得x=$\frac{|\overrightarrow{AC}|•|\overrightarrow{AB}|}{|\overrightarrow{AB}|+|\overrightarrow{AC}|}$；从而可得$\overrightarrow{AD}$=$\frac{|\overrightarrow{AC}|•|\overrightarrow{AB}|}{|\overrightarrow{AB}|+|\overrightarrow{AC}|}$（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$）
|$\overrightarrow{AB}$|=λ|$\overrightarrow{AC}$|可得$\overrightarrow{AD}$=$\frac{λ}{1+λ}$$\overrightarrow{AC}$+$\frac{1}{1+λ}$$\overrightarrow{AB}$=$\frac{λ}{1+λ}$（$\overrightarrow{c}$-$\overrightarrow{a}$）+$\frac{1}{1+λ}$（$\overrightarrow{b}$-$\overrightarrow{a}$）=$\frac{λ}{1+λ}$$\overrightarrow{c}$+$\frac{1}{1+λ}$$\overrightarrow{b}$-$\overrightarrow{a}$．

解答 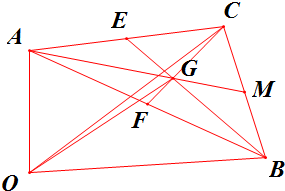解：（1）如图，
$\overrightarrow{OG}$=$\overrightarrow{OA}$+$\overrightarrow{AG}$
=$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{AM}$
=$\overrightarrow{a}$+$\frac{2}{3}$•$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）
=$\overrightarrow{a}$+$\frac{1}{3}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）
=$\overrightarrow{a}$+$\frac{1}{3}$（$\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$）
=$\overrightarrow{a}$+$\frac{1}{3}$（$\overrightarrow{b}$-$\overrightarrow{a}$+$\overrightarrow{c}$-$\overrightarrow{a}$）
=$\frac{1}{3}$（$\overrightarrow{b}$+$\overrightarrow{a}$+$\overrightarrow{c}$）；
（2）如图，
由题意，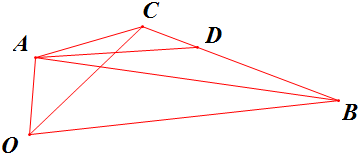
设$\overrightarrow{AD}$=x（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$）
则$\overrightarrow{CD}$=$\overrightarrow{AD}$-$\overrightarrow{AC}$=x（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$）-$\overrightarrow{AC}$
=（$\frac{x}{|\overrightarrow{AC}|}$-1）$\overrightarrow{AC}$+$\frac{x}{|\overrightarrow{AB}|}$$\overrightarrow{AB}$；
$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$=x（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$）-$\overrightarrow{AB}$
=$\frac{x}{|\overrightarrow{AC}|}$$\overrightarrow{AC}$+（$\frac{x}{|\overrightarrow{AB}|}$-1）$\overrightarrow{AB}$；
∵B、C、D三点共线，
∴$\frac{x}{|\overrightarrow{AC}|}$$\frac{x}{|\overrightarrow{AB}|}$=（$\frac{x}{|\overrightarrow{AC}|}$-1）（$\frac{x}{|\overrightarrow{AB}|}$-1）；
故x=$\frac{|\overrightarrow{AC}|•|\overrightarrow{AB}|}{|\overrightarrow{AB}|+|\overrightarrow{AC}|}$；
故$\overrightarrow{AD}$=$\frac{|\overrightarrow{AC}|•|\overrightarrow{AB}|}{|\overrightarrow{AB}|+|\overrightarrow{AC}|}$（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$）
又∵$\frac{|\overrightarrow{AB}|}{|\overrightarrow{AC}|}$=λ，∴|$\overrightarrow{AB}$|=λ|$\overrightarrow{AC}$|，
故$\overrightarrow{AD}$=$\frac{|\overrightarrow{AC}|•|\overrightarrow{AB}|}{|\overrightarrow{AB}|+|\overrightarrow{AC}|}$（$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$+$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$）
=$\frac{λ}{1+λ}$$\overrightarrow{AC}$+$\frac{1}{1+λ}$$\overrightarrow{AB}$
=$\frac{λ}{1+λ}$（$\overrightarrow{c}$-$\overrightarrow{a}$）+$\frac{1}{1+λ}$（$\overrightarrow{b}$-$\overrightarrow{a}$）
=$\frac{λ}{1+λ}$$\overrightarrow{c}$+$\frac{1}{1+λ}$$\overrightarrow{b}$-$\overrightarrow{a}$．

点评 本题考查了作图能力及平面向量运算，属于中档题．