
【题目】已知函数![]() .
.
(1)求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若方程![]() 在区间
在区间![]() 上有实根,求
上有实根,求![]() 的值;
的值;
(3)若不等式![]() 对任意正实数
对任意正实数![]() 恒成立,求正整数
恒成立,求正整数![]() 的取值集合.
的取值集合.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]() .
.
【解析】
(1)由![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)令![]() ,方程
,方程![]() 有实根等价于
有实根等价于![]() 有零点,利用导数判断函数的单调性,然后根据零点存在性定理可判断
有零点,利用导数判断函数的单调性,然后根据零点存在性定理可判断![]() 在
在![]() 和
和![]() 上分别存在一个零点,从而可得结果;
上分别存在一个零点,从而可得结果;
(3)当![]() 时,不等式成立恒成立,当
时,不等式成立恒成立,当![]() 时,不等式化为
时,不等式化为![]() ,可得
,可得![]() ,当
,当![]() 时,不等式可化为
时,不等式可化为![]() ,可得
,可得![]() ,结合(2)结合三种情况,从而可得结果.
,结合(2)结合三种情况,从而可得结果.
(1)![]()
又因为![]() ,所以切线方程为
,所以切线方程为![]()
(2)记![]() ,方程
,方程![]() 有实根等价于
有实根等价于![]() 有零点,
有零点,
因为![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
可知![]() 为极小值,又因为
为极小值,又因为![]()
所以,![]() 在
在![]() 上存在一个零点
上存在一个零点![]() ,此时
,此时![]()
又因为![]() ,
,
所以,![]() 在
在![]() 上存在一个零点
上存在一个零点![]() ,此时
,此时![]()
综上,![]() 或
或![]()
(3)不等式![]() 对任意正实数
对任意正实数![]() 恒成立,
恒成立,
即![]() ,
,![]() 恒成立,
恒成立,
当![]() 时,上式显然成立,此时
时,上式显然成立,此时![]()
当![]() 时,上式化为
时,上式化为![]() ,令
,令![]() ,
,
则![]() ,由(2)可知,函数
,由(2)可知,函数![]() 在
在![]() 上单减,且存在一个零点
上单减,且存在一个零点![]() ,此时
,此时![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以![]() 有极大值即最大值
有极大值即最大值![]() ,于是
,于是![]()
当![]() 时,不等式化为
时,不等式化为![]() ,同理可得
,同理可得![]()
综上可知,![]() ,又因为
,又因为![]() ,
,
所以正整数![]() 的取值集合为
的取值集合为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求![]() 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查居民对城市共享单车的满意度,随机选取了100人进行问卷调查,并将问卷中的100人根据其满意度评分值按照![]() 分为5组,得到号如图所示的频率分布直方图.
分为5组,得到号如图所示的频率分布直方图.
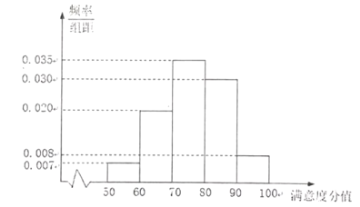
(Ⅰ)求满意度分值不低于70分的人数.
(Ⅱ)已知满意度分值在![]() 内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在
内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在![]() 的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
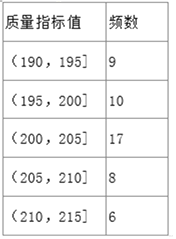
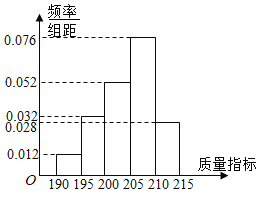
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标系与参数方程:在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上
上
(Ⅰ)求![]() 的值和直线
的值和直线![]() 的直角坐标方程及
的直角坐标方程及![]() 的参数方程;
的参数方程;
(Ⅱ)已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com