
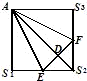
 如图在正方形AS1S2S3中,E、F分别是边S1S2、S2S3的中点,D是EF的中点,沿AE、EF、AF把这个正方形折成一个几何体,使三点S1、S2、S3重合于一点S,下面有5个结论:①AS⊥平面SEF;②AD⊥平面SEF;③SF⊥平面AEF;④EF⊥平面SAD;⑤SD⊥平面AEF.其中正确的是
如图在正方形AS1S2S3中,E、F分别是边S1S2、S2S3的中点,D是EF的中点,沿AE、EF、AF把这个正方形折成一个几何体,使三点S1、S2、S3重合于一点S,下面有5个结论:①AS⊥平面SEF;②AD⊥平面SEF;③SF⊥平面AEF;④EF⊥平面SAD;⑤SD⊥平面AEF.其中正确的是

 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:单选题
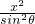 -
- =1(0<θ≤
=1(0<θ≤ ,b>0)的两个焦点,过F1的直线交双曲线的同支于A、B两点,如果|AB|=m,则△AF2B的周长的最大值是
,b>0)的两个焦点,过F1的直线交双曲线的同支于A、B两点,如果|AB|=m,则△AF2B的周长的最大值是查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 },其中
},其中 =(2x-2b,1),
=(2x-2b,1), =(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.
=(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.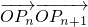 的最小值;(其中O为坐标原点)
的最小值;(其中O为坐标原点)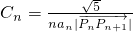 (n≥2),求:C2+C3+…+Cn的值.
(n≥2),求:C2+C3+…+Cn的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com