Question

某工厂今年一月、二月、三月生产某产品分别为1万件、1.2万件、1.3万件.为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量y与月份数x的关系，模拟函数可以选用二次函数或函数y=a·b^x+c（其中a、b、c是常数），已知四月份该产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好？请说明理由.

Answer 1

解析：先根据一月、二月、三月份的产量，求出二次函数和y=a·b^x+c（a、b、c是常数），然后看哪一个函数求出的四月份产量与实际产量1.37万件误差较小，从而可选哪个作为模拟函数.

解：设二次函数为f₁（x）=a₁x²+b₁x+c₁.

    根据题意，得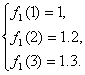

    解得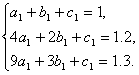

    解得a₁=-0.05，b₁=0.35，c₁=0.7.

    于是f₁（x）=-0.05x²+0.35x+0.7，

    又由y=f₂（x）=a·b^x+c，得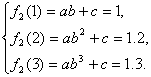

    解得a=-0.8，b=0.5，c=1.4.

    于是f₂（x）=-0.8×0.5^x+1.4，

    所以|f₁（4）-1.37|=0.07，

|f₂（4）-1.37|=0.02，

|f₁（4）-1.37|＞|f₂（4）-1.37|.

    因此，用f₂（x）=ab^x+c作模拟函数较好.