
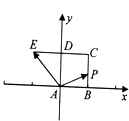
【题目】如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则下列命题正确的是 . (填上所有正确命题的序号)
,则下列命题正确的是 . (填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量 ![]() 和实数x,使
和实数x,使 ![]() =x
=x ![]() +y
+y ![]() .
.
【答案】①②
【解析】解:由题意,设正方形的边长为1,建立坐标系如图,
则B(1,0),E(﹣1,1),
∴ ![]() =(1,0),
=(1,0), ![]() (﹣1,1),
(﹣1,1),
∴ ![]() =λ
=λ ![]() +μ
+μ ![]() =(λ﹣μ,μ),
=(λ﹣μ,μ),
当点P为AD中点时,
∴ ![]() =(0,
=(0, ![]() ),
),
∴λ﹣μ=0,μ= ![]() ,
,
故λ+μ=1;故①正确,
当P∈AB时,有0≤λ﹣μ≤1,μ=0,
∴0≤λ≤1,0≤λ+μ≤1,
当P∈BC时,有λ﹣μ=1,0≤μ≤1,
∴λ=μ+1,∴1≤λ≤2,∴1≤λ+μ≤3,
当P∈CD时,有0≤λ﹣μ≤1,μ=1,
∴μ≤λ≤μ+1,即1≤λ≤2,∴2≤λ+μ≤3,
当P∈AD时,有λ﹣μ=0,0≤μ≤1,
∴0≤λ≤1,∴0≤λ+μ≤2,
综上,0≤λ+μ≤3,
故②正确;
若存在向量 ![]() 和实数x,使
和实数x,使 ![]() =x
=x ![]() +y
+y ![]() ,(y为给定的正数),
,(y为给定的正数),
则(x,0)+( ![]() ,
, ![]() )=(0,1),
)=(0,1),
即(x+ ![]() ,
, ![]() )=(0,1),
)=(0,1),
∴x+ ![]() =1,与y无关,
=1,与y无关,
故③错误,
所以答案是:①②.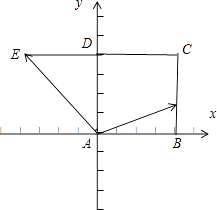
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点,需要掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某学生在假期进行某种小商品的推销,他利用所学知识进行了市场调查,发现这种商品当天的市场价格与他的进货量(件)加上20成反比.已知这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元.若每天的商品都能卖完,求这个学生一天的最大利润是多少?获得最大利润时每天的进货量是多少件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 椭圆C1:
椭圆C1: ![]() 表示的是焦点在
表示的是焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 对
对![]() ,直线
,直线![]() 与椭圆C2:
与椭圆C2: ![]() 恒有公共点.
恒有公共点.
(1)若命题“![]() ”是假命题,命题“
”是假命题,命题“![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 真
真![]() 假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
假时,求椭圆C1、椭圆C2的上焦点之间的距离d的范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出如图所示的频率分布直方图,已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[100,120]之间的学生人数是( ) 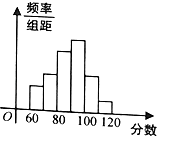
A.32
B.24
C.18
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
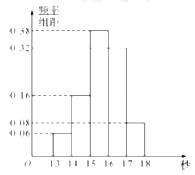
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
(Ⅰ)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均数(精确到0.1).
(Ⅱ)若从第一、五组中随机取出三名学生成绩,设取自第一组的个数为![]() ,求
,求![]() 的分布列,期望及方差.
的分布列,期望及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(α)= ![]() .
.
(1)若α为第二象限角且f(α)=﹣ ![]() ,求
,求 ![]() 的值;
的值;
(2)若5f(α)=4f(3α+2β).试问tan(2α+β)tan(α+β)是否为定值(其中α≠kπ+ ![]() ,α+β≠kπ+
,α+β≠kπ+ ![]() ,2α+β≠kπ+
,2α+β≠kπ+ ![]() ,3α+2β≠kπ+
,3α+2β≠kπ+ ![]() ,k∈Z)?若是,请求出定值;否则,说明理由.
,k∈Z)?若是,请求出定值;否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com