
(08年赤峰二中模拟理) 已知正三棱柱ABC - A1B1C1中, AA1 = 2AC = 4, 延长CB至D, 使CB = BD.
(I)求证: 直线C1B // 平面AB1D;
(II)求平面AB1D与平面ACB所成角.

解析:法一: (Ⅰ) 因为 C1B1 = CB = DB, 且C1B1 // BD,
∴ 四边形C1BDB1是平行四边形,
∴ C1B // B1D,
又B1D Ì 平面AB1D,
∴ 直线C1B // 平面AB1D.
(Ⅱ) 过B1作B1H ^ AD于H, 连结BH.
∵ B1B ^ 平面ACD,
∴ BH ^ AD
∴ Ð B1HB是平面AB1D平面ACB所成角的平面角.
在△ACD中, 由于CB = BD = BA,
∴ ∠DAC = 90°,
∴ BH =![]() AC,
AC,
∵ AA1 = 2AC = 4,
∴ tanÐB1HB =![]() = 4,
= 4,
∴ 平面AB1D平面ACB所成角为arctan4.
法二: 在△ACD中, 由于CB = BD = BA,
∴ ∠DAC=90°,
如图, 以A为原点, 以AD为x轴正向, 建立空间直角坐标系O - xyz,
∵ 正三棱柱ABC - A1B1C1中, AA1 = 2AC = 4,
∴ A(0, 0, 0), B(![]() , 1, 0), B1(
, 1, 0), B1(![]() , 1, 4),
, 1, 4),
C1(0, 2, 4), D(2![]() , 0, 0).
, 0, 0).
(Ⅰ) ∵![]() = (-
= (-![]() , 1, 4),
, 1, 4),![]() = (-
= (-![]() , 1, 4),
, 1, 4),
∴![]() //
//![]()
又BC1 Ë 平面AB1D, B1D Ì 平面AB1D,
∴ 直线C1B // 平面AB1D.
(Ⅱ) ![]() =(2
=(2![]() , 0, 0),
, 0, 0), ![]() = (
= (![]() , 1, 4), 设平面AB1D的法向量n = (x, y, z), 则
, 1, 4), 设平面AB1D的法向量n = (x, y, z), 则
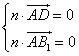 , 即
, 即 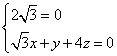 , ∴
, ∴ ![]() ,
,
取z = 1, 则n = (0, - 4, 1), 取平面ACB的法向量为m = (0, 0, 1),
则cos<n, m> =![]() ,
,




 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
(08年赤峰二中模拟理) 2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌, 保守估计中国乒乓球男队获得每枚金牌的概率均为![]() , 中国乒乓球女队获得每枚金牌的概率均为
, 中国乒乓球女队获得每枚金牌的概率均为![]() .
.
(Ⅰ) 求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;
(Ⅱ) 记中国乒乓球队获得金牌的总数为x, 按此估计求x的分布列和数学期望Ex. (结果均用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年赤峰二中模拟理) 已知F1(- 2, 0), F2 (2, 0), 点P满足| PF1| - | PF2| = 2, 记点P的轨迹为E.
(Ⅰ) 求轨迹E的方程;
(Ⅱ) 若直线l过点F2且与轨迹E交于P、Q两点,
①无论直线l绕点F2怎样转动, 在x轴上总存在定点M(m, 0), 使MP ^ MQ恒成立, 求实数m的值;
②过P、Q作直线x =![]() 的垂线PA、QB, 垂足分别为A、B, 记l =
的垂线PA、QB, 垂足分别为A、B, 记l =![]() , 求l的取值范围.
, 求l的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年赤峰二中模拟理)设函数f(x) = lnx - ax + 1.
(Ⅰ) 若函数f(x)为单调函数, 求实数a 的取值范围;
(Ⅱ) 当a > 0时, 恒有f(x) £ 0, 求a的取值范围;
(Ⅲ) 证明: ![]() ( n Î N, n ³ 2).
( n Î N, n ³ 2).
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年赤峰二中模拟文) 已知如图椭圆![]() 为其右焦点,A为左顶点,椭圆的右准线方程为
为其右焦点,A为左顶点,椭圆的右准线方程为![]() ,长轴长为4.过F的直线
,长轴长为4.过F的直线![]() 与椭圆交于异于A的P、Q两点.
与椭圆交于异于A的P、Q两点.
(1)求椭圆方程;
(2)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com