
【题目】已知椭圆C: ![]() =1(a>b>0)过点(
=1(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),且离心率为
),且离心率为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点A(x1 , y1),B(x2 , y2)是椭圆C上的亮点,且x1≠x2 , 点P(1,0),证明:△PAB不可能为等边三角形.
科目:高中数学 来源: 题型:
【题目】某网站对“爱飞客”飞行大会的日关注量x(万人)与日点赞量y(万次)进行了统计对比,得到表格如下:
x | 3 | 5 | 6 | 7 | 9 |
y | 2 | 3 | 3 | 4 | 5 |
由散点图象知,可以用回归直线方程 ![]() 来近似刻画它们之间的关系.
来近似刻画它们之间的关系.
(Ⅰ)求出y关于x的回归直线方程,并预测日关注量为10万人时的日点赞量;
(Ⅱ)一个三口之家参加“爱飞客”亲子游戏,游戏规定:三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球,大人摸出每个红球得奖金10元,小孩摸出1个红球得奖金50元.求该三口之家所得奖金总额不低于50元的概率.
参考公式:b= 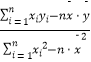 ; 参考数据:
; 参考数据: ![]() =200,
=200, ![]() =112.
=112.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理科答)已知数列{an}及等差数列{bn},若a1=3,an= ![]() an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
(1)证明数列{an﹣2}为等比数列;
(2)求数列{an}及数列{bn}的通项公式;
(3)设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体ABCD﹣A1B1C1D1中,E,F分别是棱B1C1 , C1D1的中点. (Ⅰ)求AD1与EF所成角的大小;
(Ⅱ)求AF与平面BEB1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83. 
(1)求x和y的值;
(2)计算甲班7位学生成绩的方差s2;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是椭圆E: ![]() =1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与E相交于A,B两点,且|AB|=
=1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与E相交于A,B两点,且|AB|= ![]() (Ⅰ)求E的离心率
(Ⅰ)求E的离心率
(Ⅱ)设点P(0,﹣1)满足|PA|=|PB|,求E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为(1,0),A,B是抛物线上位于x轴两侧的两动点,且 ![]() =﹣4(O为坐标原点).
=﹣4(O为坐标原点).
(1)求抛物线方程;
(2)证明:直线AB过定点T;
(3)过点T作AB的垂线交抛物线于M,N两点,求四边形AMBN的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com