
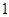 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;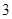 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率; 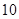 的等边
的等边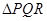 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形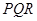 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形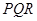 内。求弹孔与
内。求弹孔与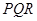 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).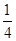 (2)
(2)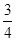 (3)
(3)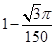
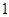 次,共有4个基本事件。
次,共有4个基本事件。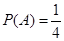 .
. 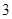 次,前三枪共有4个基本事件:{0,1,2},{0,1,3},{0,2,3},{1,2,3};
次,前三枪共有4个基本事件:{0,1,2},{0,1,3},{0,2,3},{1,2,3};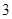 次,这三枪中出现空弹”的事件为B,
次,这三枪中出现空弹”的事件为B,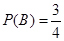 。
。 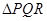 的面积为
的面积为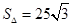 ,
, 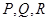 为圆心、1为半径的三个扇形的面积和为:
为圆心、1为半径的三个扇形的面积和为: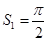 ,
, 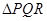 三个顶点的距离都大于1”的事件为C,
三个顶点的距离都大于1”的事件为C,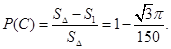


科目:高中数学 来源:不详 题型:解答题
 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出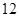 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:| 班级 | 高三(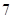 )班 )班 | 高三(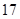 )班 )班 | 高二(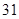 )班 )班 | 高二(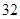 )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A. 1-a-b | B.1-a·b |
| C.(1-a)·(1-b) | D.1-(1-a)·(1-b) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.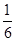 | B.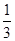 | C.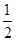 | D.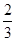 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
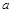 表示第1枚骰子出现的点数,
表示第1枚骰子出现的点数,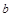 表示第2枚骰子出现的点数.
表示第2枚骰子出现的点数.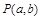 满足
满足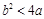 的概率;
的概率;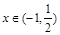 时,求函数
时,求函数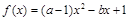 为单调函数的概率.
为单调函数的概率. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com