
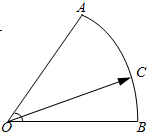
 如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若
如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若 =x
=x +y
+y ,则x+3y的取值范围是________.
,则x+3y的取值范围是________.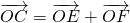 ,结合平面向量基本定理得到
,结合平面向量基本定理得到 =x
=x ,
, =y
=y .考虑到x、y均为正数且x+3y中y的系数较大,所以当y越大时x+3y的值越大,因此将点C沿AB弧由A向B运动,加以观察即可得到x+3y的取值范围.
.考虑到x、y均为正数且x+3y中y的系数较大,所以当y越大时x+3y的值越大,因此将点C沿AB弧由A向B运动,加以观察即可得到x+3y的取值范围.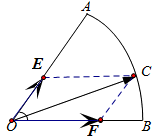 过点C作CE∥OB,交OA于E,再作CF∥OA,交OB于F,可得
过点C作CE∥OB,交OA于E,再作CF∥OA,交OB于F,可得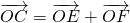
 =x
=x +y
+y ,
, 与
与 是共线向量且
是共线向量且 与
与 是共线向量,
是共线向量, =x
=x ,
, =y
=y
 与
与 同向、
同向、 与
与 同向,可得x=
同向,可得x=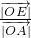 且y=
且y=
 |变短而|
|变短而| |变长
|变长 =x
=x +y
+y 的情况下求x+3y的取值范围.着重考查了平面向量基本定理、向量的线性运算法则和二元函数最值求法等知识,属于中档题.
的情况下求x+3y的取值范围.着重考查了平面向量基本定理、向量的线性运算法则和二元函数最值求法等知识,属于中档题. 

科目:高中数学 来源: 题型:
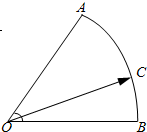 (2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若
(2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若| OC |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,
如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,| OC |
| OA |
| OB |
查看答案和解析>>
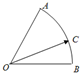
科目:高中数学 来源:不详 题型:单选题
| OC |
| OA |
| OB |
A.(
| B.(1,3) | C.(
| D.(
|
查看答案和解析>>
科目:高中数学 来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷01(理科)(解析版) 题型:选择题
 ,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )
,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com