设数列{a
n}是等差数列,{b
n}是各项均为正数的等比数列,且a
1=b
1,a
3+b
5=21,a
5+b
3=13,
(1)求数列{a
n},{b
n}的通项公式;
(2)若数列{
}的前n项和为S
n,试比较S
n与4的大小关系.
(1)设{a
n}的公差为d,{b
n}的公比为q,则依题意有q>0且
解得d=2,q=2.
所以a
n=1+(n-1)d=2n-1,b
n=q
n-1=2
n-1.
(2)
=.
Sn=1+++++,①
∴
2Sn=2+3++++,②
②-①得
Sn=2+2++++-=
2+2×(1++++)-=
2+2×-=
6-.
S
n-4=
2-,
由S
n-4<0得出2
n<2n+3,解得n=1,2,3,
由S
n-4>0得出2
n>2n+3,解得n=4,5,6,….
所以当n≤3时S
n<4,当n≥4时S
n>4.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
设数列{a
n}是等差数列,数列{b
n}是各项都为正数的等比数列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1与a
4的等差中项.
(I)求数列{a
n},{b
n}的通项公式;
(II)求数列{
}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2012•枣庄一模)设数列{a
n}满足a
1=1,a
2=2,对任意的n∈N
*,a
n+2是a
n+1与a
n的等差中项.
(1)设b
n=a
n+1-a
n,证明数列{b
n}是等比数列,并求出其通项公式;
(2)写出数列{a
n}的通项公式(不要求计算过程),令
cn=n(-an),求数列{c
n}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年四川省成都市望子成龙学校高二(上)期中数学试卷(解析版)
题型:解答题
设数列{a
n}是等差数列,数列{b
n}是各项都为正数的等比数列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1与a
4的等差中项.
(I)求数列{a
n},{b
n}的通项公式;
(II)求数列{
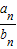
}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省临沂市重点高中高二(上)期末数学试卷(理科)(解析版)
题型:解答题
设数列{a
n}是等差数列,数列{b
n}是各项都为正数的等比数列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1与a
4的等差中项.
(I)求数列{a
n},{b
n}的通项公式;
(II)求数列{
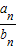
}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年四川省成都市望子成龙学校高二(上)期中数学试卷(解析版)
题型:解答题
设数列{a
n}是等差数列,数列{b
n}是各项都为正数的等比数列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1与a
4的等差中项.
(I)求数列{a
n},{b
n}的通项公式;
(II)求数列{
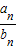
}的前n项和S
n.
查看答案和解析>>



 阅读快车系列答案
阅读快车系列答案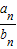 }的前n项和Sn.
}的前n项和Sn.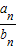 }的前n项和Sn.
}的前n项和Sn.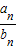 }的前n项和Sn.
}的前n项和Sn.