在△ABC中,AB边所在直线方程是2x-y+3=0,BC边上的高所在直线方程是x=1,且顶点C的坐标是(3,-1).
(1)求点A的坐标;
(2)求AC边所在直线的方程;
(3)求△ABC的面积S.
【答案】
分析:先按题意作出示意图,由图形探究问题的解法
(1)由图知,点A的是AB边所在直线与直线是x=1的交点,联立两个直线的方程求出点A的坐标;
(2)由(1)及点C的坐标,故可由两点式求出AC的方程;
(3)BC边上的高所在直线方程是x=1知,BC的斜率是0,可得出直线BC的方程是y=-1,解出点B的坐标,即可求出BC的长度,又点A到BC的距离易知,由公式求出三角形的面积
解答: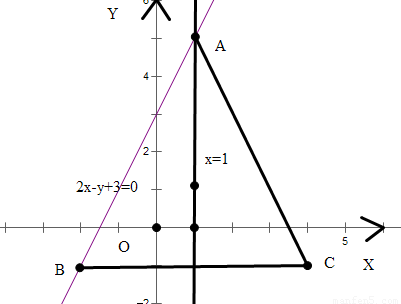
解:(1)作出如图的示意图
由于点A的是AB边所在直线与直线是x=1的交点,令
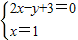
,
解得x=1,y=5
故A(1,5)
(2)由(1)及顶点C的坐标是(3,-1).得直线AC的方程是
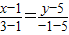
整理得3x+y-8=0
即直线AC的方程是3x+y-8=0
(3)令
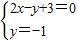
得x=-2,
故B(-2,-1)
所以BC的长度是5,又A到BC的距离是6,故三角形ABC的面积是
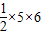
=15
点评:本题考查求两直线的交点,求直线的方程的方法,求三角形的面积,解题的关键是熟练掌握求交点坐标的方法,直线方程的种形式,本题的重点是求交点的坐标,难点是根据已知条件选择合适的求直线方程的公式

 解:(1)作出如图的示意图
解:(1)作出如图的示意图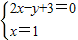 ,
,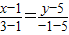
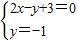 得x=-2,
得x=-2,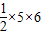 =15
=15

 名校课堂系列答案
名校课堂系列答案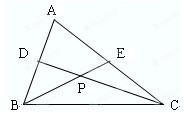 如图,在△ABC中,AB=
如图,在△ABC中,AB=