
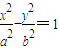 (a>0,b>0)的左、右焦点分别为F1、F2,抛物线C2:x2=-2py(p>0)的焦点为F,C1与C2的一个交点为A,知A在x轴上的射影为F1,且A、F、F2三点共线,则双曲线C1的离心率为 .
(a>0,b>0)的左、右焦点分别为F1、F2,抛物线C2:x2=-2py(p>0)的焦点为F,C1与C2的一个交点为A,知A在x轴上的射影为F1,且A、F、F2三点共线,则双曲线C1的离心率为 . 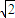 p;再结合A在双曲线上以及a2+b2=c2即可求出双曲线C1的离心率.
p;再结合A在双曲线上以及a2+b2=c2即可求出双曲线C1的离心率.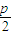 ).
).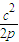 ).
). ⇒
⇒ ⇒c=
⇒c=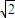 p ①.
p ①.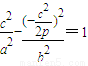 ②
②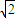 a.
a.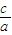 =
=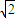 .
.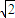 .
.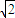 p.
p. 

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.-1 B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.-1 B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2011年天津市滨海新区高考数学模拟试卷(文科)(解析版) 题型:填空题
 (a>0,b>0)的左、右焦点分别为F1、F2,抛物线C2的顶点在原点,它的准线与双曲线C1的左准线重合,若双曲线C1与抛物线C2的交点P满足PF2⊥F1F2,则双曲线C1的离心率为 .
(a>0,b>0)的左、右焦点分别为F1、F2,抛物线C2的顶点在原点,它的准线与双曲线C1的左准线重合,若双曲线C1与抛物线C2的交点P满足PF2⊥F1F2,则双曲线C1的离心率为 .查看答案和解析>>
科目:高中数学 来源:2011年天津市滨海新区高三联考数学试卷(理科)(解析版) 题型:填空题
 (a>0,b>0)的左、右焦点分别为F1、F2,抛物线C2的顶点在原点,它的准线与双曲线C1的左准线重合,若双曲线C1与抛物线C2的交点P满足PF2⊥F1F2,则双曲线C1的离心率为 .
(a>0,b>0)的左、右焦点分别为F1、F2,抛物线C2的顶点在原点,它的准线与双曲线C1的左准线重合,若双曲线C1与抛物线C2的交点P满足PF2⊥F1F2,则双曲线C1的离心率为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com