
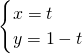 (t为参数)和C2:ρ+2sinθ=0上的动点,则M、N两点间的最小距离是________.
(t为参数)和C2:ρ+2sinθ=0上的动点,则M、N两点间的最小距离是________. -1
-1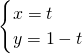 消去t可得x+y-1=0,由点到直线的距离公式,结合几何意义可得答案.
消去t可得x+y-1=0,由点到直线的距离公式,结合几何意义可得答案.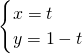 消去t可得x+y-1=0,
消去t可得x+y-1=0,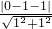 =
= ,故M、N两点间的最小距离是
,故M、N两点间的最小距离是 ,
,


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
 |
| AB |
查看答案和解析>>
科目:高中数学 来源:安徽省合肥168中学2010届高三第一次月考数学理学科试题 题型:044
在直角坐标系xoy中,以o为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(![]() -
-![]() )=1,M、N分别为曲线C与x轴,y轴的交点.
)=1,M、N分别为曲线C与x轴,y轴的交点.
(1)写出曲线C的直角坐标方程,并求M、N的极坐标;
(2)设MN中点为P,求直线OP的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
选修 4- 4 :极坐标与参数方程
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,M , N分别为曲线C与x轴,y轴的交点.
,M , N分别为曲线C与x轴,y轴的交点.
(1)写出曲线C的直角坐标方程,并求M , N的极坐标;
(2)设M , N的中点为P,求直线OP的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
选修 4- 4 :极坐标与参数方程
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,M , N分别为曲线C与x轴,y轴的交点.
,M , N分别为曲线C与x轴,y轴的交点.
(1)写出曲线C的直角坐标方程,并求M , N的极坐标;
(2)设M , N的中点为P,求直线OP的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com