解:(1)∵
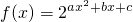
过(0,8),(-1,1),(1,16)三点,
∴
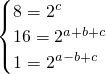
,即:
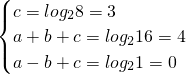
,
解方程组得:
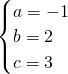
,
∴
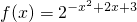
.
(2)∵
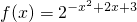
对于任意x∈R都有意义,
∴
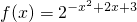
的定义域为R.
设u=-x
2+2x+3,则f(x)=2
u,
当x∈R时,由二次函数性质知u∈(-∞,4],
所以f(x)=2
u,u∈(-∞,4],
根据f(x)=2
u为指函数性质可知:f(x)∈(-∞,16].
(3)由(2)知:设u=-x
2+2x+3,则f(x)=2
u,u∈(-∞,4]
①当x∈(-∞,1]时,随x增大,u增大,
从指数函数性质知:随u增大,f(x)=2
u也增大,
所以
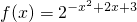
在(-∞,1]上为增函数.
②当x∈[1,+∞)时,随x增大,u减小,
从指数函数性质知:随u减小,f(x)=2
u也减小,
所以
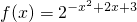
在(-∞,1]上为减函数.
分析:(1)把(0,8),(-1,1),(1,16)三点分别代入
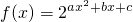
,能够求出f(x)的解析式.
(2)由
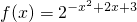
对于任意x∈R都有意义,知
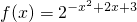
的定义域为R.设u=-x
2+2x+3,则f(x)=2
u,利用二次函数的性质求出u∈(-∞,4],再由指函数性质能求出f(x)的值域.
(3)设u=-x
2+2x+3,则f(x)=2
u,u∈(-∞,4],利用复合函数的单调性的性质,能求出f(x)的单调区间.
点评:本题考查函数的解析式、定义域、值域和单调区间的求法,解题时要认真审题,注意待定系数法、换元法、二次函数的性质和指数函数的性质的灵活运用.

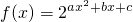
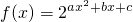 过(0,8),(-1,1),(1,16)三点,
过(0,8),(-1,1),(1,16)三点,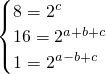 ,即:
,即: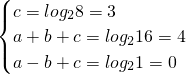 ,
,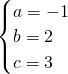 ,
,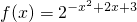 .
.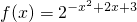 对于任意x∈R都有意义,
对于任意x∈R都有意义,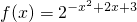 的定义域为R.
的定义域为R.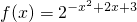 在(-∞,1]上为增函数.
在(-∞,1]上为增函数.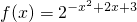 在(-∞,1]上为减函数.
在(-∞,1]上为减函数.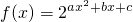 ,能够求出f(x)的解析式.
,能够求出f(x)的解析式.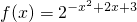 对于任意x∈R都有意义,知
对于任意x∈R都有意义,知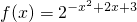 的定义域为R.设u=-x2+2x+3,则f(x)=2u,利用二次函数的性质求出u∈(-∞,4],再由指函数性质能求出f(x)的值域.
的定义域为R.设u=-x2+2x+3,则f(x)=2u,利用二次函数的性质求出u∈(-∞,4],再由指函数性质能求出f(x)的值域.

 名校课堂系列答案
名校课堂系列答案