
甲同学在军训中,练习射击项目,他射击命中目标的概率是 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.
(Ⅰ)在3次射击中,求甲至少有1次命中目标的概率;
(Ⅱ)在射击中,若甲命中目标,则停止射击,否则继续射击,直至命中目标,但射击次数最多不超过3次,求甲射击次数的分布列和数学期望.
(Ⅰ)解:记“在3次射击中,甲至少有1次命中目标”为事件A。 1分
则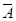 表示事件“在3次射击中,甲没有命中目标。”
2分
表示事件“在3次射击中,甲没有命中目标。”
2分
故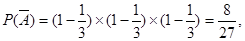 4分
4分
所以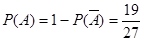 。 6分
。 6分
(Ⅱ)解:记甲的射击次数为X,则X的可能取值为1,2,3 7分
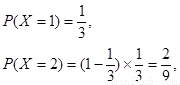
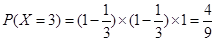 10分
10分
X的分布列为:
|
X |
1 |
2 |
3 |
|
P |
|
|
|
11分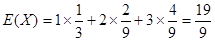 (环)。
13分
(环)。
13分
【解析】本试题朱亚奥是考查了独立重复试验中事件发生的概率的运用。以及二项分布的概率的运用。
(1)因为射击命中目标的概率是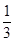 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.
则在3次射击中,求甲至少有1次命中目标的概率可以根据对立事件的概率求解得到。
(2)那么先分析随机变量各个取值的情况,得到各个取值的概率值得到求解。


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市西城区(北区)高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com