分析:(1)根据阅读内容提供的方法,设
f(x)=()x+()x,将不等式变形并利用f(x)的单调性和f(1)=1,即可求出原不等式的解集;
(2)方程的两边同除以13
x,得(
)
x+(
)
x=1,利用函数
g(x)=()x+()x的单调性和g(2)=1,即可证出原方程有唯一解x=2.
解答:解:(1)由9
x>5
x+4
x,两边同除以9
x可得
1≥()x+()x.
∵
0<<<1,∴函数
f(x)=()x+()x在R上为单调减函数,
∵
f(1)=+=1,
∴当x>1时,f(x)=
()x+()x<f(1)=1,
因此,原不等式的解集为{x|x>1}.
(2)方程有唯一解x=2,证明如下:
将方程两边同除以13
x,可得(
)
x+(
)
x=1,
∵
0<<<1,可得函数g(x)=(
)
x+(
)
x在R上为单调减函数,
∵
g(2)=()2+()2=1,
∴当x>2时,g(x)=(
)
x+(
)
x<g(2),即(
)
x+(
)
x<1;
且当x<2时,g(x)=(
)
x+(
)
x>g(2),(
)
x+(
)
x>1.
由此可得,有且仅有x=2能使等式成立,即x=2为方程5
x+12
x=13
x的唯一解.
点评:本题给出解关于x的指数方程的例题,要求我们根据该例题解关于x的指数方程和不等式.着重考查了指数函数的单调性和类比推理的一般方法等知识,属于中档题.



 ,函数
,函数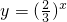 和
和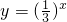 在R内都单调递减;则f(x)在(-∞,+∞)内单调递减.
在R内都单调递减;则f(x)在(-∞,+∞)内单调递减. .
.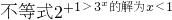 ;
;