
【题目】设函数![]() .
.
(1)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的最小值;
的最小值;
(2)讨论函数![]() 零点的个数;
零点的个数;
(3)若对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() 时,函数
时,函数![]() 有两个零点;(3)
有两个零点;(3)![]() .
.
【解析】
试题(1)当m=e时,![]() >0,由此利用导数性质能求出f(x)的极小值;(2)由
>0,由此利用导数性质能求出f(x)的极小值;(2)由![]() ,得
,得![]() ,令
,令![]() ,x>0,m∈R,则h(1)=
,x>0,m∈R,则h(1)=![]() ,
,
h′(x)=1-x2=(1+x)(1-x),由此利用导数性质能求出函数g(x)=f′(x)-![]() 零点的个数;(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围
零点的个数;(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围
试题解析:(1)由题设,当![]() 时,
时,![]()
易得函数![]() 的定义域为
的定义域为![]()
![]()
![]() 当
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增;
上单调递增;
![]() 当
当![]() 时,
时,![]() 取得极小值
取得极小值![]()
![]()
![]() 的极小值为2
的极小值为2
(2)![]() 函数
函数![]()
令![]() ,得
,得![]()
设![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() 是
是![]() 的唯一极值点,且是极大值点,因此x=1也是
的唯一极值点,且是极大值点,因此x=1也是![]() 的最大值点,
的最大值点,
![]()
![]() 的最大值为
的最大值为![]()
又![]() ,结合y=
,结合y=![]() 的图像(如图),可知
的图像(如图),可知
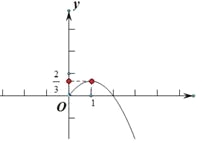
①当![]() 时,函数
时,函数![]() 无零点;
无零点;
②当![]() 时,函数
时,函数![]() 有且仅有一个零点;
有且仅有一个零点;
③当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
④![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
综上所述,当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
(3)对任意![]() 恒成立,等价于
恒成立,等价于![]() 恒成立
恒成立
设![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
![]() 在
在![]() 恒成立
恒成立
![]() 恒成立
恒成立
![]() (对
(对![]() ,
,![]() 仅在
仅在![]() 时成立),
时成立),![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古建筑中的窗饰是艺术和技术的统一体,给人于美的享受.如图(1)为一花窗;图(2)所示是一扇窗中的一格,呈长方形,长30 cm,宽26 cm,其内部窗芯(不含长方形边框)用一种条形木料做成,由两个菱形和六根支条构成,整个窗芯关于长方形边框的两条对称轴成轴对称.设菱形的两条对角线长分别为x cm和y cm,窗芯所需条形木料的长度之和为L.
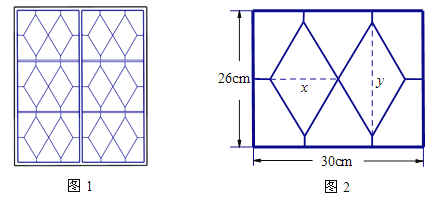
(1)试用x,y表示L;
(2)如果要求六根支条的长度均不小于2 cm,每个菱形的面积为130 cm2,那么做这样一个窗芯至少需要多长的条形木料(不计榫卯及其它损耗)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 和抛物线
和抛物线![]() :
: ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)已知直线![]() 和圆
和圆![]() 相切,与抛物线
相切,与抛物线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过抛物线![]() 上一点
上一点![]() 作两直线
作两直线![]() 和圆
和圆![]() 相切,且分别交抛物线
相切,且分别交抛物线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且椭圆
,且椭圆![]() 上任意一点到
上任意一点到![]() 点的最大距离为
点的最大距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 长轴上的一点,求
长轴上的一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,其上顶点为
,其上顶点为![]() ,右顶点和右焦点分别为
,右顶点和右焦点分别为![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),
),![]() ,试判定直线
,试判定直线![]() 是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知曲线
轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),射线
),射线![]() ,
,![]() ,
,![]() 分别与曲线
分别与曲线![]() 交于极点
交于极点![]() 外的三点
外的三点![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 两点在曲线
两点在曲线![]() 上,求
上,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com