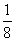练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已已知请根据上述两个等式计算cos(α-β)与cos(α+β)的值.

    解:将已知两式平方后相加,得

    2+2(sinαsinβ+cosαcosβ)=+,

    cosαcosβ+sinαsinβ=-,

    ∴cos(α-β)=-.

    将已知两式平方后相减,结合cos(α-β)=-,

    得=cos2α-sin2α+cos2β-sin2β+2(cosαcosβ-sinαsinβ)=cos2α+cos2β+2cos(α+β)

    =cos［(α+β)+(α-β)］+cos［(α+β)-(α-β)］+2cos(α+β)

    =2cos(α+β)·cos(α-β)+2cos(α+β)

    =cos(α+β),∴cos(α+β)=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：数学教研室 题型：044

    已知命题：如果a、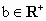，且a＋b=1，那么．

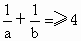    ①证明这个命题是真命题；

    ②根据已知条件，还能得到什么新的不等式？试写出其中两个，并加以证明；

    ③如果a、b、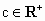，且a＋b＋c=1，推广上述已知命题，能得到什么不等式？请加以证明；

    ④如果，且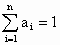，推广上述已知命题，能得到什么不等式？请加以证明．

    查看答案和解析>>

    同步练习册答案