
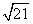 )作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4,
)作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4,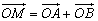 ,求
,求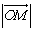 的最小值(O为坐标原点)。
的最小值(O为坐标原点)。  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年浙江省高三上学期提前班期中考试理科数学 题型:解答题
(本题满分15分) 圆C过点A(2,0)及点B(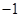 ,
,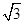 ),且与直线l:y=
),且与直线l:y=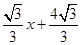 相切
相切
(1)求圆C的方程;
(2)过点P(2,1)作圆C的切线,切点为M,N,求|MN|;
(3)点Q为圆C上第二象限内一点,且∠BOQ=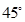 ,求Q点横坐标.
,求Q点横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4. =
= +
+ ,求|
,求| |的最小值(O为坐标原点).
|的最小值(O为坐标原点).查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市余姚中学高二(上)第一次质量检测数学试卷(文科)(解析版) 题型:解答题
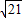 ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.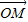 =
=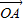 +
+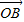 ,求|
,求| |的最小值(O为坐标原点).
|的最小值(O为坐标原点).查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省福州市文博中学高三(上)期中数学试卷(文科)(解析版) 题型:解答题
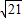 ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4.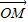 =
= +
+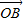 ,求|
,求|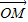 |的最小值(O为坐标原点).
|的最小值(O为坐标原点).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com