
①y=sinx+tanx-x ②y=sin2x+cosx ③y=(cosx+|cosx|)sinx ④y=3sin2(x+![]() )
)
A.0个 B.1个 C.2个 D.3个
解析:①定义域是x∈R,且x≠![]() +kπ,k∈Z,关于原点对称,且f(-x)=sin(-x)+tan(-x)+x=-sinx-tanx+x=-f(x),
+kπ,k∈Z,关于原点对称,且f(-x)=sin(-x)+tan(-x)+x=-sinx-tanx+x=-f(x),
∴y=sinx+tanx-x为奇函数.
②定义域为x∈R,关于原点对称,且f(-x)=[sin(-x)]2+cos(-x)=sin2x+cosx=f(x),∴y=sin2x+cosx为偶函数.
③定义域x∈R,关于原点对称,且f(-x)=[cos(-x)+|cos(-x)|]sin(-x)=-(cosx+|cosx|)·sinx=-f(x),∴y=(cosx+|cos|x)sinx为奇函数
④y=3sin(2x+![]() )=3cos2x为偶函数,故应选A.
)=3cos2x为偶函数,故应选A.
答案:A


科目:高中数学 来源:数学教研室 题型:013
下列函数中:①y=sinx+tanx-x;② ;③y=sin|x|;④
;③y=sin|x|;④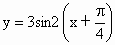 ,属于非奇非偶函数的有
,属于非奇非偶函数的有
[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com