精英家教网 > 高中数学 > 题目详情

若f(x)=

，现用随机模拟的方法估计y=f（x）与x=4及x轴围成的面积S，用计算机先产生两组（每组30个）在区间[0，4]上的均匀随机数x₁，x₂，…，x₃₀和y₁，y₂，…，y₃₀，由此得到30个点（x_i，y_i）（i=1，2，…，30），现数出其中满足y_i≤f（x_i）（i=1，2，…，30）的点有10个，则由随机模拟的方法可估计得到面积S为（　　）

A．6

B．

C．

D．5

分析：本题是用随机模拟的方法估算不规则图形的面积，若不规则图形的面积为S，模拟实验点的产生区域为Ω，则P≈

，结合实验所得频数与实验总次数，估算出频率，即得答案．

解答：解：在区间[0，4]上的均匀随机数x₁，x₂，…，x₃₀和y₁，y₂，…，y₃₀，
由此得到30个点（x_i，y_i）（i=1，2，…，30），
即所有基本事件Ω共有30个
而其中满足y_i≤f（x_i）（i=1，2，…，30）的点有10个，
即满足条件基本事件共有10个
则y=f（x）与x=4及x轴围成的面积S满足

4×4

≈

即S≈

故选B

点评：本题考查的知识点是随机模拟实验，其中当不规则图形的面积为S，模拟实验点的产生区域为Ω时，则P≈

是解任本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

某工厂因排污比较严重，决定着手整治，一个月时污染度为60，整治后前四个月的污染度如表：

月数	1	2	3	4	…
污染度	60	31	13	0	…

污染度为0后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：f（x）=20|x-4|（x≥1），g(x)=

(x-4)2(x≥1)，h(x)=

240

|log2x-

|(x≥1)，其中x表示月数，f（x）、g（x）、h（x）分别表示污染度．
（1）问选用哪个函数模拟比较合理？并说明理由；
（2）若以比较合理的模拟函数预测，整治后有多少个月的污染度不超过60？

查看答案和解析>>

科目：高中数学 来源： 题型：

一化工厂因排污趋向严重，2011年1月决定着手整治．经调研，该厂第一个月的污染度为60，整治后前四个月的污染度如下表；

月数	1	2	3	4	…
污染度	60	31	13	0	…

污染度为0后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：f（x）=20|x-4|（x≥1），g（x）=

(x-4)2(x≥1)，h（x）=30|log₂x-2|（x≥1），其中x表示月数，f（x），g（x），h（x）分别表示污染度．（参考数据：lg2=0.3010，lg3=0.4771）
（Ⅰ）问选用哪个函数模拟比较合理，并说明理由；
（Ⅱ）如果环保部门要求该厂每月的排污度均不能超过60，若以比较合理的模拟函数预测，该厂最晚在何时开始进行再次整治？

查看答案和解析>>

科目：高中数学 来源： 题型：

5．A解析：因为函数有0，1，2三个零点，可设函数为f(x)=ax(x-1)(x-2)=ax3-3ax2+2ax

因此b=-3a,又因为当x>2时f(x)>0所以a>0,因此b<0

在15个村庄中有7个村庄交通不方便，现从中任意选10个，用X表示这10个村庄中交通方便的村庄数，若，则a= .

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

一化工厂因排污趋向严重，2011年1月决定着手整治．经调研，该厂第一个月的污染度为60，整治后前四个月的污染度如下表；
月数 1 2 3 4 …
污染度 60 31 13 0 …
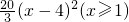污染度为0后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：f（x）=20|x-4|（x≥1），g（x）= $数学公式$ ，h（x）=30|log₂x-2|（x≥1），其中x表示月数，f（x），g（x），h（x）分别表示污染度．（参考数据：lg2=0.3010，lg3=0.4771）
（Ⅰ）问选用哪个函数模拟比较合理，并说明理由；
（Ⅱ）如果环保部门要求该厂每月的排污度均不能超过60，若以比较合理的模拟函数预测，该厂最晚在何时开始进行再次整治？

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学