
分析 (1)由题意求出椭圆方程,
(2)然后求出和OA平行且和椭圆相切的直线方程,把切点到直线OA的距离转化为原点O到切线的距离,则三角形AOB面积的最大值可求.
解答 解(1):由题意$\frac{c}{a}=\frac{\sqrt{2}}{2}$,$\frac{{b}^{2}}{a}=\sqrt{2}$,a2=b2+c2
解得a=2$\sqrt{2}$,b=c=2,
则椭圆的方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$
(2)要使△AOB面积最大,则B到OA所在直线距离最远.
设与OA平行的直线方程为y=$\frac{\sqrt{2}}{2}x+b$.
由$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x+b}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$消去y并化简得.x2+$\sqrt{2}b$x+b2-4=0.
由△=0得b=±2$\sqrt{2}$,
不妨取b>0,
∴与直线OA平行,且与椭圆相切且两直线方程为:y=$\frac{\sqrt{2}}{2}x+2\sqrt{2}$,
则B到直线OA的距离等于O到直线:y=$\frac{\sqrt{2}}{2}x+2\sqrt{2}$,
的距离d,d=$\frac{4\sqrt{3}}{3}$,又|OA|=$\sqrt{6}$,
△AOB面积的最大值s=$\frac{1}{2}×\sqrt{6}×\frac{4\sqrt{3}}{3}=2\sqrt{2}$.
点评 本题考查了椭圆方程的求法,考查了直线和圆锥曲线的位置关系,体现了数学转化思想方法,是中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (1,2) | C. | (1,-2) | D. | (-1,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | ±1 | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
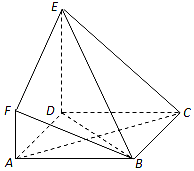 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角为45°.
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角为45°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com