
 ,
, .且
.且 ∥
∥ ,求f(x)的值;
,求f(x)的值;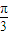 <A+
<A+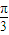 <π,然后求出函数f(A)的取值范围.
<π,然后求出函数f(A)的取值范围.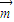 ∥
∥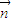 ,得
,得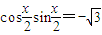
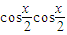 ,∴
,∴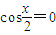 或
或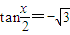 ,∴x=2kπ+π或
,∴x=2kπ+π或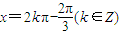 ,∴
,∴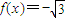
 ,B=
,B=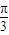 ,∴0<A<
,∴0<A<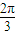 .∴
.∴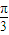 <A+
<A+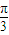 <π,0<sin(A+
<π,0<sin(A+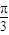 )≤1.
)≤1.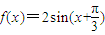 ,∴故函数f(A)的取值范围是(0,2].
,∴故函数f(A)的取值范围是(0,2].

科目:高中数学 来源:2008-2009学年高三(上)数学寒假作业(理科)(解析版) 题型:解答题
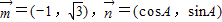 ;且
;且 .
.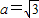 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.查看答案和解析>>
科目:高中数学 来源:2008-2009学年高三(上)数学寒假作业(文科)(解析版) 题型:解答题
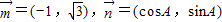 ;且
;且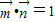 .
.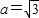 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.查看答案和解析>>
科目:高中数学 来源:江苏省南通中学高三数学纠错训练2(解析版) 题型:解答题
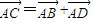 ,则ABCD为平行四边形
,则ABCD为平行四边形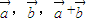 为非零向量,且a+b平分a与b的夹角,则|a|=|b|
为非零向量,且a+b平分a与b的夹角,则|a|=|b|查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com