
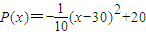 (万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数:
(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数: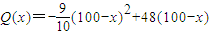 (万元).
(万元).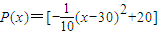 ,新产品投入的年利润为
,新产品投入的年利润为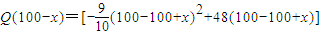
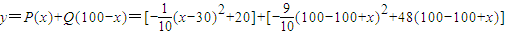


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
| 1 |
| 10 |
| 9 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)为了解决资金缺口,第一年初向银行贷款1 000万元,利率为5.5%(不计复利),第五年底一次性应向银行偿还本息共计多少万元?
(2)从新产品投产的第三年开始,从100万元的生产准备金中,新旧两种产品各应投入多少万元,才能使年利润最大?
(3)从新旧产品的五年总利润中最高拿出70%来,能否还清对银行的欠款?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
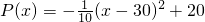 (万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数:
(万元).现准备开发一个回报率高,科技含量高的新产品从“十一五”计划(此计划历时5年)的第一年开始,用两年的时间完成.这两年,每年从100万元的生产准备金中拿出80万元投入新产品的开发,从第三年开始这100万元就可全部用于新旧两种产品的生产投入.经预测,新产品每年投入x万元,可获得的年利润表示为函数: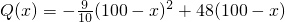 (万元).
(万元).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 10 |
| 9 |
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com