
某选修课的考试按A级、B级依次进行,只有当A级成绩合格时,才可继续参加B级的考试.已知每级考试允许有一次补考机会,两个级别的成绩均合格方可获得该选修课的合格证书.现某人参加这个选修课的考试,他A级考试成绩合格的概率为 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得该选修课的合格证书的概率;
(2)在这个考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求
,求 的数学期望E
的数学期望E .
.
(1) ,(2)
,(2)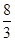 .
.
解析试题分析:(1)解概率问题,关键明确事件所包含的意义. 不需要补考就获得合格证书的事件为A级第一次考试合格且B级第一次考试合格,因为事件相互独立,所以由概率乘法得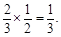 (2)参加考试的次数至少2次,至多4次,因此
(2)参加考试的次数至少2次,至多4次,因此 =2,3,4,因为不放弃所有的考试机会,所以
=2,3,4,因为不放弃所有的考试机会,所以 =2包含①A级第一次考试合格且B级第一次考试合格,②A级第一次考试不合格且A级补考不合格。
=2包含①A级第一次考试合格且B级第一次考试合格,②A级第一次考试不合格且A级补考不合格。 =4包含A级第一次考试不合格且A级补考合格, B级第一次考试不合格,B级补考合格或不合格.
=4包含A级第一次考试不合格且A级补考合格, B级第一次考试不合格,B级补考合格或不合格.  =3包含事件较多,可利用
=3包含事件较多,可利用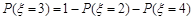 求解,最后再利用数学期望公式求E
求解,最后再利用数学期望公式求E .
.
试题解析:设“A级第一次考试合格”为事件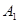 ,“A级补考合格”为事件A2; “B级第一次考试合格”为事件
,“A级补考合格”为事件A2; “B级第一次考试合格”为事件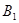 ,“B级补考合格”为事件
,“B级补考合格”为事件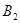 .
.
(1)不需要补考就获得合格证书的事件为A1·B1,注意到A1与B1相互独立,
则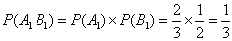
答:该考生不需要补考就获得合格证书的概率为 4
4
(2)由已知得, =2,3,4,注意到各事件之间的独立性与互斥性,可得
=2,3,4,注意到各事件之间的独立性与互斥性,可得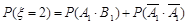
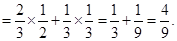 .6
.6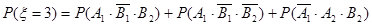
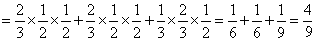 .8
.8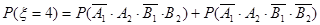
 .10
.10
故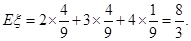
答:该考生参加考试次数的期望为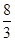 .13
.13
考点:古典概型概率,分布列及数学期望


科目:高中数学 来源: 题型:解答题
(2013•天津)一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4; 白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率.
(2)再取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.4.用击中环数的期望与方差比较两名射手的射击水平.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲向靶子A射击两次,乙向靶子射击一次.甲每次射击命中靶子的概率为0.8,命中得5分;乙命中靶子的概率为0.5,命中得10分.
(1)求甲、乙二人共命中一次目标的概率;
(2)设X为二人得分之和,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设X为学生甲在三道程序中获优的次数,求X的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
盒子里装有16只球,其中6只是玻璃球,另外10只是木质球.而玻璃球中有2只是红色的,4只是蓝色的;木质球中有3只是红色的,7只是蓝色的,现从中任取一只球,如果已知取到的是蓝色的球,求这个球是玻璃球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com