练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求由抛物线，直线所围成的图形的面积.


    解 由，得抛物线与轴的交点坐标是和，所求图形分成两块，

    分别用定积分表示面积

    ，.

    故面积=

    ==.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数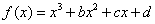的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为．

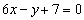    （Ⅰ）求函数y=f(x)的解析式；

    （Ⅱ）求函数y=f(x)的单调区间．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


      设函数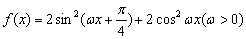的图象上两个相邻的最低点之间的距离为.

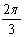      (1)求函数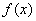的最大值，并求出对应的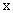值；

     （2）若函数的图象向右平移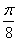个单位长度，再沿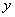轴翻折后得到.求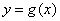的单调递减区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若复数 ()是纯虚数，则=          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲方是一农场，乙方是一工厂，由于乙方生产须占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付的情况下，乙方的年利润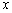（元）与年产量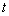（吨）满足函数关系 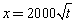．若乙方每生产一吨产品必须赔付甲方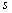元（以下称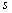为赔付价格）．

    （1）将乙方的年利润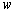（元）表示为年产量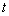（吨）的函数，并求出乙方获得最大利润的年产量；

    （2）甲方每年受乙方生产影响的经济损失金额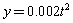（元），在乙方按照获得最大利润的产量进行生产

    的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格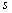是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列程序框图的输出结果为

    A.          B.   C.          D.

                     i>2013?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数．

    （Ⅰ）求不等式的解集；

    （Ⅱ），使，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图．

    图1－6

    将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．

    (1)根据已知条件完成下面的2×2列联表，并据此资料你是否认为“体育迷”与性别有关？

     

     

    非体育迷

    体育迷

    合计

    男

    a

    b

    女

    c

    d=10

    55

    合计

    n

    (2)将上述调查所得到的频率视为概率．现在从该地区大量电视观众中．采用随机抽样方法每次抽取1名观众，抽取3次．记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的，求X的分布列，期望E(X)和方差D(X)．

    附：χ2＝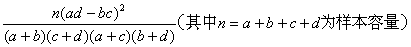

    P(χ2≥k)

    0.05

    0.01

    k

    3.841

    6.635

     

    查看答案和解析>>

    同步练习册答案