练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列满足：所有的奇数项构成以1为首项，1为公差的等差数列；所有的偶数项构成以2为首项，3为公差的等差数列，则（   ）

    A．200            B．201           C．400     　   D．402

     

    【答案】

    A

    【解析】由题意得

    200.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}是各项均不为0的等差数列，Sn为其前n项和，且满足an2=S2n-1，令bn=
    1an•an+1
    ，数列{bn}的前n项和为Tn．
    （1）求数列{an}的通项公式及数列{bn}的前n项和为Tn；
    （2）是否存在正整数m，n（1＜m＜n），使得T1，Tm，Tn成等比数列？若存在，求出所有的m，n的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}满足an=2an-1+2n-1(n≥2)，a1=5，bn=
    an-1
    2n
    ．
    （Ⅰ）证明：{bn}为等差数列；
    （Ⅱ）求数列{an}的前n项和Sn；
    （Ⅲ）设cn=
    9
    bnbn+1
    ，求数列{cn}的前n项和Tn，并求使Tn＞
    1
    4
    (m2-5m)    对所有的n∈N*都成立的最大正整数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•武汉模拟）已知数列{an}满足：a1=a2=a3=k，an+1=
    k+anan-1
    an-2
    (n≥3，n∈N*)    其中k＞0，数列{bn}满足：bn=
    an+an+2
    an+1
    (n=1，2，3，4…)
    （1）求b1，b2，b3，b4；
    （2）求数列{bn}的通项公式；
    （3）是否存在正数k，使得数列{an}的每一项均为整数，如果不存在，说明理由，如果存在，求出所有的k．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （13分）已知数列满足：其中，数列满足：

       （1）求；

       （2）求数列的通项公式；

       （3）是否存在正数k，使得数列的每一项均为整数，如果不存在，说明理由，如果存在，求出所有的k.

    查看答案和解析>>

    科目：高中数学 来源：河北省石家庄一中09-10学年度高一第二学期高一期中考试 题型：单选题

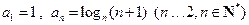    已知数列满足．定义：使
    乘积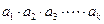为正整数的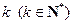叫做“和谐数”，则在区间
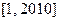    内所有的“和谐数”的和为

    A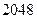．B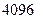．C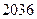．D．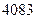

    查看答案和解析>>

    同步练习册答案