
【题目】已知函数f(x)= ![]() ,曲线y=f(x)在点(e2 , f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).
,曲线y=f(x)在点(e2 , f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).
(1)求f(x)的解析式及单调递减区间;
(2)若存在x0∈[e,+∞),使函数g(x)=aelnx+ ![]() lnxf(x)≤a成立,求实数a的取值范围.
lnxf(x)≤a成立,求实数a的取值范围.
【答案】
(1)解:函数f(x)的定义域为(0,1)∪(1,+∞),f′(x)= ![]() ,
,
又由题意有: ![]() =
= ![]() ,所以m=2,f(x)=
,所以m=2,f(x)= ![]() .
.
此时,f′(x)= ![]() ,由f′(x)<0得0<x<1或1<x<e,
,由f′(x)<0得0<x<1或1<x<e,
所以函数f(x)的单调递减区间为(0,1)和(1,e).
(2)解:因为g(x)=aelnx+ ![]() ﹣(a+e)x,
﹣(a+e)x,
由已知,若存在x0∈[e,+∞),使函数g(x)=aelnx+ ![]() lnxf(x)≤a成立,
lnxf(x)≤a成立,
则只需满足当x∈[e,+∞),g(x)min≤a即可.
又g(x)=aelnx+ ![]() ﹣(a+e)x,
﹣(a+e)x,
则g′(x)= ![]() ,
,
a≤e,则g′(x)≥0在x∈[e,+∞)上恒成立,
∴g(x)在[e,+∞)上单调递增,
∴g(x)min=g(e)=﹣ ![]() ,
,
∴a≥﹣ ![]() ,
,
∵a≤e,
∴﹣ ![]() ≤a≤e.
≤a≤e.
a>e,则g(x)在[e,a)上单调递减,在[a,+∞)上单调递增,
∴g(x)在[e,+∞)上的最小值是g(a),
∵g(a)<g(e),a>e,∴满足题意,
综上所述,a≥﹣ ![]() .
.
【解析】(1)由题意有: ![]() =
= ![]() ,可得f(x)的解析式;由f′(x)<0得0<x<1或1<x<e,即可求出单调递减区间;(2)由已知,若存在x0∈[e,+∞),使函数g(x)=aelnx+
,可得f(x)的解析式;由f′(x)<0得0<x<1或1<x<e,即可求出单调递减区间;(2)由已知,若存在x0∈[e,+∞),使函数g(x)=aelnx+ ![]() lnxf(x)≤a成立,则只需满足当x∈[e,+∞),g(x)min≤a即可
lnxf(x)≤a成立,则只需满足当x∈[e,+∞),g(x)min≤a即可
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE. 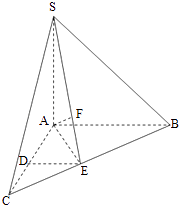
(1)求证:AF⊥平面SBC;
(2)在线段上DE上是否存在点G,使二面角G﹣AF﹣E的大小为30°?若存在,求出DG的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足4千步为不健康生活方式,不少于16千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为200人,高一学生人数为700人,高二学生人数600人,高三学生人数500,从中抽取n人作为调查对象,得到了如图所示的这n人的频率分布直方图,这n人中有20人被学校界定为不健康生活方式者. 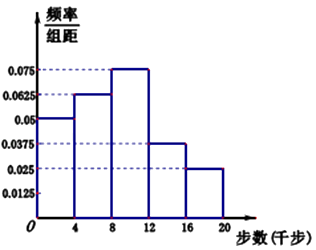
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取3人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励0元,超健康生活方式者表彰奖励20元,一般生活方式者鼓励性奖励10元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1; 
(1)求二面角C﹣PB﹣E的余弦值;
(2)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个判断: ①某校高三一班和高三二班的人数分别是m,n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为 ![]() ;
;
②10名工人某天生产同一零件的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
③从总体中抽取的样本为 ![]() ,则回归直线
,则回归直线 ![]() 必过点(
必过点( ![]() )
)
④已知ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤0)=4,则P(ξ>2)=0.2
其中正确的个数有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三第一学期期末四校联考数学第I卷中共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准规定:“每题只选一项,答对得5分,不答或答错得0分.”某考生每道题都给出一个答案,已确定有5道题的答案是正确的,而其余选择题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求出该考生:
(1)得40分的概率;
(2)得多少分的可能性最大?
(3)所得分数ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kex﹣x2(其中k∈R,e是自然对数的底数).
(Ⅰ)若k<0,试判断函数f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若k=2,当x∈(0,+∞)时,试比较f(x)与2的大小;
(Ⅲ)若函数f(x)有两个极值点x1 , x2(x1<x2),求k的取值范围,并证明0<f(x1)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以![]() 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数
,存在一个正数![]() ,使得函数
,使得函数![]() 的值域包含于区间
的值域包含于区间![]() .例如,当
.例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() .现有如下命题:
.现有如下命题:
①设函数![]() 的定义域为
的定义域为![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”;
”;
②函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值;
有最大值和最小值;
③若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,
,![]() ,则
,则![]() ;
;
④若函数![]() (
(![]() ,
,![]() )有最大值,则
)有最大值,则![]() .
.
其中的真命题有 .(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com