
已知等腰三角形腰上的中线长为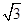 ,则该三角形的面积的最大值为 ▲ .
,则该三角形的面积的最大值为 ▲ .
3/5
【解析】解:根据题意画出图形,如图所示:
设AB=AC=2a,由D是AB的中点,得到AD=DB=a,
在△ADC中,根据余弦定理得:cosA=a2+4a2-3 2×a×2a =5a2-3 /4a2 ,解得a2=3 /(5-4cosA ),
设△ADC的面积为S,
则S=1 /2 a•2a•sinA=a2sinA=3sinA /5-4cosA ①,
.下研究求面积的最值
法一:求导得:S′=3cosA(5-4cosA)-12sin2A (5-4cosA)2 =15cosA-12 (5-4cosA)2 ,令S′=0,解得cosA=4/ 5 ,
当cosA<4 /5 时,S′>0,S单调递增;当cosA>4 /5 时,S′<0,S单调递减,
所以S在cosA=4 5 处取极大值,且极大值为最大值,此时sinA=3 /5


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:2014届四川省绵阳市高二12月月考理科数学试卷(解析版) 题型:选择题
已知等腰三角形腰上的中线长为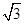 ,则该三角形的面积的最大值为( )
,则该三角形的面积的最大值为( )
A.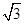 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com