
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为![]() 和
和![]() .
.
求:(1)有且只有甲一人译出密码的概率;
(2)甲和乙至多有一人译出密码的概率;
(3)若要使译出密码的概率不小于![]() ,而且全用像乙这样的人,问至少需要多少人?
,而且全用像乙这样的人,问至少需要多少人?
解:记“甲译出密码”为事件A,“甲译不出密码”为事件![]() ;“乙译出密码”为事件B,“乙译不出密码”为事件
;“乙译出密码”为事件B,“乙译不出密码”为事件![]() .
.
(1)“有且只有甲一人译出密码”为事件A1,则由于甲、乙两人独立地破译密码,为相互独立事件,所以事件A1发生是指事件A和B同时发生,从而有P(A1)=P(A·![]() )=P(A)·P(
)=P(A)·P(![]() )=
)=![]() ×(1-
×(1-![]() )=
)=![]() .
.
(2)“甲和乙至多有一人译出密码”为事件A2,则事件![]() 的对立事件是“甲、乙两人都译出密码”,即A2=A·B.从而有P(A2)=1-P(
的对立事件是“甲、乙两人都译出密码”,即A2=A·B.从而有P(A2)=1-P(![]() )=1-P(A·B)=1-P(A)·P(B)=1-
)=1-P(A·B)=1-P(A)·P(B)=1-![]() ×
×![]() =
=![]() .
.
(3)设至少需要n个人,则由于n个像乙这样的人都译不出密码的概率为(1-![]() )n,根据题意,得n个像乙这样的人译出密码的概率满足1-(1-
)n,根据题意,得n个像乙这样的人译出密码的概率满足1-(1-![]() )n≥
)n≥![]() ,即3n≥100(n∈N*).
,即3n≥100(n∈N*).
解得n≥5,且n∈N*.因此需要像乙这样的人至少5人.


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 4 |
| 99 |
| 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
求:(1)两人都译出密码的概率;
(2)两人都译不出密码的概率;
(3)恰有1人译出密码的概率;
(4)至多有1人译出密码的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为![]() 和
和![]() ,求
,求
(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为![]() ,至少需要多少乙这样的人.
,至少需要多少乙这样的人.
查看答案和解析>>
科目:高中数学 来源:2015届河南郑州盛同学校高一下学期第一次月考数学试卷(解析版) 题型:解答题
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为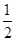 和
和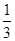 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高二下学期期末考试文科数学卷 题型:解答题
(本小题满分12分)
甲、乙两人独立地破译一份密码,甲能破译出密码的概率是1/3,乙能破译出密码的概率是1/4,试求:
①甲、乙两人都译不出密码的概率;
②甲、乙两人中恰有一人能译出密码的概率;
③甲、乙两人中至多有一人能译出密码的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com