
已知函数f(x)=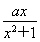 +a,g(x)=aln x-x(a≠0).
+a,g(x)=aln x-x(a≠0).
(1)求函数f(x)的单调区间;
(2)求证:当a>0时,对于任意x1,x2∈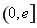 ,总有g(x1)<f(x2)成立.
,总有g(x1)<f(x2)成立.
(1)当a>0时,f(x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);当a<0时,f(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).(2)见解析
【解析】(1)函数f(x)的定义域为R,
f′(x)= .
.
当a>0时,当x变化时,f′(x),f(x)的变化情况如下表:
x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
f′(x) | - | 0 | + | 0 | - |
f(x) | ↘ |
| ↗ |
| ↘ |
当a<0时,当x变化时,f′(x),f(x)的变化情况如下表:
x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ |
| ↘ |
| ↗ |
综上所述,当a>0时,f(x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);当a<0时,f(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
(2)证明:由(1)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,且f(e)=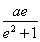 +a>a=f(0).
+a>a=f(0).
所以x∈(0,e]时,f(x)>f(0)=a.
因为g(x)=aln x-x,所以g′(x)=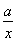 -1,
-1,
令g′(x)=0,得x=a.
①当0<a<e时,由g′(x)>0,得0<x<a;由g′(x)<0,得x>a,所以函数g(x)在(0,a)上单调递增,在(a,e]上单调递减,
所以g(x)max=g(a)=aln a-a.
因为a-(aln a-a)=a(2-ln a)>a(2-ln e)=a>0,
所以对于任意x1,x2∈(0,e],总有g(x1)<f(x2).
②当a≥e时,g′(x)≥0在(0,e]上恒成立,
所以函数g(x)在(0,e]上单调递增,g(x)max=g(e)=a-e<a,
所以对于任意x1,x2∈(0,e],仍有g(x1)<f(x2).
综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f(x2).


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(解析版) 题型:选择题
甲、乙两位射击运动员,甲击中环数X1~B(10,0.9),乙击中环数X2=2Y+1,其中Y~B(5,0.8),那么下列关于甲、乙两运动员平均击中环数的说法正确的是( )
A.甲平均击中的环数比乙平均击中的环数多
B.乙平均击中的环数比甲平均击中的环数多
C.甲、乙两人平均击中的环数相等
D.仅依据上述数据,无法判断谁击中的环数多
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集8讲练习卷(解析版) 题型:解答题
在△ABC中,内角A,B,C所对的边分别为a,b,c,且f(A)=2cos 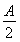 sin
sin +sin2
+sin2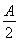 -cos2
-cos2 .
.
(1)求函数f(A)的最大值;
(2)若f(A)=0,C= ,a=
,a= ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集7讲练习卷(解析版) 题型:填空题
图表示的是函数y=Asin(ωx+φ)(ω>0,-π<φ<π)的图像的一段,O是坐标原点,P是图像的最高点,M点的坐标为(5,0),若| |=
|= ,
, ·
· =15,则此函数的解析式为________.
=15,则此函数的解析式为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集7讲练习卷(解析版) 题型:选择题
将函数y=sin 的图像上各点向右平移
的图像上各点向右平移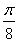 个单位,则得到新函数的解析式为( )
个单位,则得到新函数的解析式为( )
A.y=sin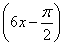 B.y=sin
B.y=sin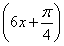 C.y=sin
C.y=sin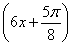 D.y=sin
D.y=sin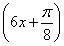
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集6讲练习卷(解析版) 题型:选择题
已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”.下列函数中,有“巧值点”的是( )
①f(x)=x2;②f(x)=e-x;③f(x)=ln x;④f(x)=tan x;⑤f(x)= .
.
A.①③⑤ B.③④ C.②③④ D.②⑤
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集5讲练习卷(解析版) 题型:选择题
如图所示,图(1)反映的是某条公共汽车线路收支差额y与乘客量x之间关系的图像.由于目前该条公交线路亏损,公司有关人员提出两种调整建议,如图(2)(3)所示.
(注:收支差额=营业所得的票价收入-付出的成本)

给出以下说法:
①图(2)的建议是:提高成本,并提高票价;
②图(2)的建议是:降低成本,并保持票价不变;
③图(3)的建议是:提高票价,并保持成本不变;
④图(3)的建议是:提高票价,并降低成本.
其中说法正确的序号是( )
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集3A讲练习卷(解析版) 题型:选择题
已知关于x的不等式ax2+2x+b>0(a≠0)的解集是 ,且a>b,则
,且a>b,则 的最小值是( )
的最小值是( )
A.2 B.2 C.
B.2 C. D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com