
分析 由题意可得t=($\frac{1}{2}$)x∈[$\frac{1}{4}$,8],换元可得y=t-$\frac{1}{2}$)2+$\frac{3}{4}$,由二次函数可得.
解答 解:∵x∈[-3,2],∴t=($\frac{1}{2}$)x∈[$\frac{1}{4}$,8],
换元可得y=($\frac{1}{4}$)x-($\frac{1}{2}$)x+1=t2-t+1=(t-$\frac{1}{2}$)2+$\frac{3}{4}$,
由二次函数可知y在t∈[$\frac{1}{4}$,$\frac{1}{2}$]单调递减,在t∈[$\frac{1}{2}$,8]单调递增,
∴当t=$\frac{1}{2}$时,函数取最小值$\frac{3}{4}$,当t=8时,函数取最大值57
故答案为:[$\frac{3}{4}$,57]
点评 本题考查二次函数在闭区间的最值,涉及换元法和指数函数的性质,属基础题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 40 | 50 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 70 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
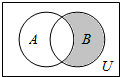 设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )
设全集U=R,集合A={x|$\frac{x-3}{x+2}$=0},B={x|x2-x-6=0},则阴影部分所表示的集合是( )| A. | {3} | B. | {-2} | C. | {3,-2} | D. | {∅} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com