
如图所示,在矩形ABCD中,且AB=1,BC=a,现沿AC折成二面角D-AC-B,使BD⊥AD,BD⊥BC.
(1)求证:平面ABD⊥平面ABC;
(2)a为何值时,二面角D-AC-B为45°?
(3)a为何值时,异面直线AC与BD所成的角为60°?

|
如图,(1)∵AD⊥CD,AD⊥BD, ∴AD⊥面BCD, ∴BC⊥AD,又BC⊥BD, ∴BC⊥平面ABD,而BCÌ 面ABC,故面ABD⊥面ABC
(2)∵面ABD⊥面ABC,作DE⊥AB于E,则 DE ⊥面ABC,作EF⊥AC于F,可证明AC⊥DF,∴∠ DFE为二面角D-AC-B的平面角.在 Rt△ADC中,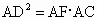 ,∴ ,∴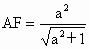 , ,
又 Rt△AEC∽Rt△ABC,∴ 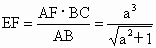 , ,
在 Rt△ADC中,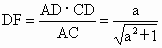 , ,
在 Rt△DEF中,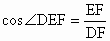 , ,
即 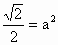 ,∴ ,∴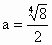 . .
(3) 作BM⊥AC于M过点B作BN∥AC与FE的延长线交于点N,则BMFN为矩形,且BN⊥DN.于是∠DBN为异面直线AC与BD所成的角.∵ 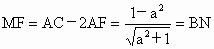 , ,
在 Rt△CBD中,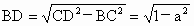 . .
在 Rt△BND,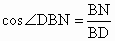 , ,
即 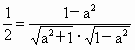 ,解之得 ,解之得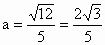 . .
|
|
第(1)问易证,第(2)问和第(3)问要分别作出平面角和线线角,然后建立含a的方程即可.本题是有关面面角、线线角的逆向问题,关键是作出这些角,然后归结为解有关三角形,难点是计算三角形中有关的线段长. |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
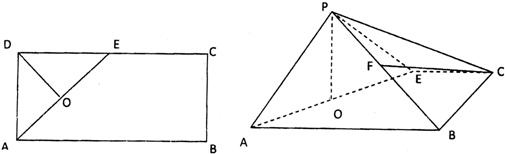 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
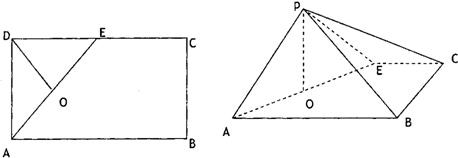
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com