
(本题满分12分)已知函数 .
.
(Ⅰ)用分段函数的形式表示 ,并求
,并求 的最大值;
的最大值;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)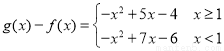 ,最大值是
,最大值是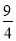 ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)分x≥1,x<1可去掉绝对值,得到g(x)﹣f(x)的表达式,再考虑各段的最值,即可得到函数的最大值;
(Ⅱ)讨论x≥1时,x<1时的g(x)≥f(x)的解集,注意运用二次不等式的解法,最后再求并集.
试题解析:(Ⅰ)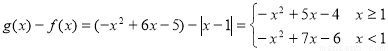 4分
4分
由函数图象可知,g(x)-f(x)的最大值在[1,4]上取得,
∴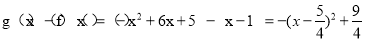 ,
,
∴当x=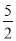 时,g(x)-f(x)取到最大值是
时,g(x)-f(x)取到最大值是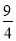 . 6分
. 6分
(Ⅱ)当x≥1时,f(x)=x-1;
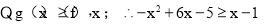 7分
7分
整理,得(x-1)(x-4)≤0,
解得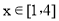 ; 8分
; 8分
当x<1时,f(x)=1-x;
∵g(x)≥f(x),
∴ , 9分
, 9分
整理,得(x-1)(x-6)≤0,
解得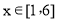 ,
,
又 ,所以不等式组无解 10分
,所以不等式组无解 10分
综上,x的取值范围是[1,4]. 12分
考点:分段函数的应用.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源:2012-2013学年安徽省高三上学期第二次模拟考试理科数学试卷(解析版) 题型:填空题
已知命题 ,命题
,命题 ,若非p是非q的必要不充分条件,那么实数m的取值范围是 .
,若非p是非q的必要不充分条件,那么实数m的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com