
【题目】求下列函数的单调递减区间:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,圆
,圆![]() ,已知直线
,已知直线![]() 与圆
与圆![]() 相切,且与抛物线
相切,且与抛物线![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求直线![]() 在
在![]() 轴上截距
轴上截距![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 是抛物线的焦点,
是抛物线的焦点,![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD中,边长为2,E为AB中点,F是边BC上的动点.
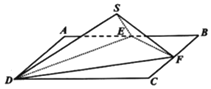
(1)将△ADE沿DE翻折90°到△SDE,求二面角S-DC-E的正切值;
(2)若![]() ,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求
,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在中国首都北京举行,会议期间,达成了多项国际合作协议.假设甲、乙两种品牌的同类产品出口某国家的市场销售量相等,该国质量检验部门为了解他们的使用寿命,现从这两种品牌的产品中分别随机抽取300个进行测试,结果统计如下图所示,已知乙品牌产品使用寿命小于200小时的概率估计值为![]() .
.
(1)求![]() 的值;
的值;
(2)估计甲品牌产品寿命小于200小时的概率;
(3)这两种品牌产品中,某个产品已使用了200小时,试估计该产品是乙品牌的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强,以上正确说法的个数是( )
之间的负相关很强,以上正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)令![]() .
.
①当![]() 时,若函数
时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
②当![]() 时,若
时,若![]() 的解集为
的解集为![]() ,且
,且![]() 中有且仅有一个整数,求实数b的取值范围.
中有且仅有一个整数,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com