
分析 (1)甲乙两人各摸一次球就终止的含意为甲先摸,摸到的是黑球,乙后摸,摸到的是白球,此时X=2,由此能求出甲乙两人各摸一次球就终止的概率.
(2)袋中的7个球 3白4黑,随机变量X的所有可能取值是1,2,3,4,5.分别求出相的应的概率,由此能求出随机变量X的概率分布列和E(X).
解答 解:(1)甲乙两人各摸一次球就终止的含意为甲先摸,摸到的是黑球,乙后摸,摸到的是白球,此时X=2,
由题P(X=2)=$\frac{{A}_{4}^{1}{A}_{3}^{1}}{{A}_{7}^{2}}$=$\frac{2}{7}$,
∴甲乙两人各摸一次球就终止的概率为$\frac{2}{7}$.…(4分)
(2)袋中的7个球 3白4黑,随机变量X的所有可能取值是1,2,3,4,5.
P(X=1)=$\frac{{A}_{3}^{1}}{{A}_{7}^{1}}$=$\frac{3}{7}$,
P(X=2)=$\frac{{A}_{4}^{1}{A}_{3}^{1}}{{A}_{7}^{2}}$=$\frac{2}{7}$,
P(X=3)=$\frac{{A}_{4}^{2}{A}_{3}^{1}}{{A}_{7}^{4}}$=$\frac{6}{35}$,
P(X=4)=$\frac{{A}_{4}^{3}{A}_{3}^{1}}{{A}_{7}^{4}}$=$\frac{3}{35}$,
P(X=5)=$\frac{{A}_{4}^{4}{A}_{3}^{1}}{{A}_{7}^{5}}$=$\frac{1}{35}$.…(12分)
(注:此段(4分)的分配是每错1个扣(2分),错到4个即不得分,另用其它解法酌情给分)
随机变量X的概率分布列为:
| X | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{7}$ | $\frac{2}{7}$ | $\frac{6}{35}$ | $\frac{3}{35}$ | $\frac{1}{35}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:选择题
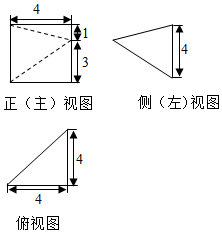 一锥体的三视图如图所示,设该棱锥的最长棱和最短棱的棱长分别为m,n,则$\frac{m}{n}$等于( )
一锥体的三视图如图所示,设该棱锥的最长棱和最短棱的棱长分别为m,n,则$\frac{m}{n}$等于( )| A. | $\frac{\sqrt{33}}{4}$ | B. | $\frac{\sqrt{41}}{3}$ | C. | $\frac{\sqrt{41}}{4}$ | D. | $\frac{\sqrt{33}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-3i | B. | 1+3i | C. | -1+3i | D. | -1-3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | [2,3) | C. | $({\frac{9}{4},3})$ | D. | $[{\frac{9}{4},3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com