
分析 把函数f(x)=x3-3x-a在x∈[$-\frac{1}{2}$,$\sqrt{3}$]内有零点,转化为a在函数y=x3-3x(x∈[$-\frac{1}{2},\sqrt{3}$])的值域内.
利用导数求出函数y=x3-3x在[$-\frac{1}{2}$,$\sqrt{3}$]上的最值求得p:$a∈[-2,\frac{11}{8}]$.再由函数g(x)=x2-alnx在区间$(0,\frac{a}{2})$内是减函数,得g′(x)=2x-$\frac{a}{x}$=$\frac{2{x}^{2}-a}{x}$(x>0)在$(0,\frac{a}{2})$内小于等于0恒成立,由此求出q:a∈(0,2].然后分p真q假和p假q真求得实数a的取值范围.
解答 解:函数f(x)=x3-3x-a在x∈[$-\frac{1}{2}$,$\sqrt{3}$]内有零点,
等价于a在函数y=x3-3x(x∈[$-\frac{1}{2},\sqrt{3}$])的值域内.
由y′=3x2-3,可知当x∈[$-\frac{1}{2}$,1)时,y′<0,当x∈(1,$\sqrt{3}$]时,y′>0,
∴y=x3-3x在[$-\frac{1}{2}$,$\sqrt{3}$]上的极小值为-2,又当x=-$\frac{1}{2}$时,y=$\frac{11}{8}$,当x=$\sqrt{3}$时,y=0.
∴p:$a∈[-2,\frac{11}{8}]$.
函数g(x)=x2-alnx在区间$(0,\frac{a}{2})$内是减函数.
则g′(x)=2x-$\frac{a}{x}$=$\frac{2{x}^{2}-a}{x}$(x>0)在$(0,\frac{a}{2})$内小于等于0恒成立,
∴$\sqrt{\frac{a}{2}}$≥$\frac{a}{2}$,则0≤a≤2,又a>0,
∴q:a∈(0,2].
当p真q假时,a∈[-2,0],当p假q真时,$a∈(\frac{11}{8},2]$.
综上,a的取值范围为[-2,0]∪$(\frac{11}{8},2]$.
点评 本题考查命题的真假判断与应用,考查了函数零点的判断方法,训练了利用导数求函数的最值,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
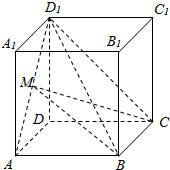 如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )
如图,已知正方体ABCD-A1B1ClD1的棱长为a,点M为线段AD1的中点.三棱锥D1-BMC的正视图面积等于( )| A. | $\frac{1}{2}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{2}{a}^{2}}{4}$ | D. | $\frac{\sqrt{3}{a}^{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$ | B. | $\frac{11}{10}$ | C. | $\frac{12}{11}$ | D. | $\frac{13}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com