练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如果关于x的方程a(b－c)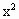＋b(c－a)x＋c(a－b)＝0有两个相等的实根(abc≠0)，求证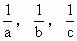：成等差数列．

    答案：
    解析：

    当x＝1时，a(b－c)＋b(c－a)＋c(a－b)＝0，又方程有两个相等的实根，∴＝1，于是＝1，∴c(a－b)＝a(b－c)，即2ac＝ab＋bc，两边同除以abc，得．∴，，成等差数列．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知定义在区间[-
    π
    2
    ，π]    上的函数y=f（x）的图象关于直线x=
    π
    4
    对称，当x≥
    π
    4
    时，函数f（x）=sinx．
    （Ⅰ）求f(-
    π
    2
    )    ，f(-
    π
    4
    )    的值；
    （Ⅱ）求y=f（x）的函数表达式；
    （Ⅲ）如果关于x的方程f（x）=a有解，那么将方程在a取某一确定值时所求得的所有解的和记为Ma，求Ma的所有可能取值及相对应的a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设非零向量
    a
    与
    b
    的夹角为θ，|
    b
    | =
    		2
    |
    a
    |    ，如果关于x的方程x2-2|
    a
    | x+
    a
    •
    b
    =0    有实根，那么θ的范围是
    [45°，180°]．
    [45°，180°]．
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•宁波模拟）如果关于x的方程
    		x-1
    =kx    在区间[1，5]上有解，则有（　　）

    查看答案和解析>>

    科目：高中数学 来源：高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型：044

    如果关于x的方程a(b－c)x2＋b(c－a)x＋c(a－b)＝0有两个相等的实数根(abc≠0)，求证：，，成等差数列．

    查看答案和解析>>

    同步练习册答案