
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) 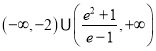
【解析】
(1)根据导数的几何意义可知,![]() 在
在![]() 的导数是曲线在
的导数是曲线在![]() 处切线的斜率,列方程求
处切线的斜率,列方程求![]() ;(2)不等式变形为
;(2)不等式变形为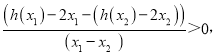 设
设![]() ,可得
,可得![]() 递增,所以
递增,所以![]() 在
在![]() 恒成立,
恒成立,
变形为![]() 恒成立,转化为求函数的最值;(3)不等式
恒成立,转化为求函数的最值;(3)不等式![]() 等价于
等价于![]() ,设
,设![]() ,求
,求![]() ,然后讨论极值点和定义域的关系,分
,然后讨论极值点和定义域的关系,分![]() ,
,![]() 和
和![]() 三种情况求函数在
三种情况求函数在![]() 上的最小值,令最小值小于0,分别解关于
上的最小值,令最小值小于0,分别解关于![]() 的不等式,得到
的不等式,得到![]() 的取值范围.
的取值范围.
(1)![]() 的导数为
的导数为![]() ,曲线
,曲线![]() 在
在![]() 处的切线斜率为
处的切线斜率为![]() ,
,
由切线的方程为![]() ,可得
,可得![]() ,
,
解得![]() ;
;
(2)![]() ,
,
对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,即为
恒成立,即为
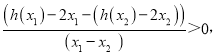
令![]() ,可得
,可得![]() 递增,
递增,
由![]() 恒成立,
恒成立,
可得![]() 的最大值,由
的最大值,由![]() 可得最大值
可得最大值![]() ,
,
则![]() ,即
,即![]() 的取值范围是
的取值范围是![]() ;
;
(3)不等式![]() 等价于,
等价于,![]()
整理得![]() ,设
,设![]() ,
,
则由题意可知只需在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() .
.
对![]() 求导数,得
求导数,得![]()
因为![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() .
.
①若![]() ,即
,即![]() 时,令
时,令![]() ,解得
,解得![]() .
.
②若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 处取得最小值,
处取得最小值,
令![]() ,即
,即![]() ,
,
可得![]()
对于式子![]() ,因为
,因为![]() ,可得左端大于
,可得左端大于![]() ,而右端小于
,而右端小于![]() ,所以不等式不能成立
,所以不等式不能成立
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,只需
上单调递减,只需![]() ,得
,得![]() ,
,
又因为![]() ,则
,则![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是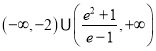 .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】如图是由正整数构成的数表,用aij表示i行第j个数(i,j∈N+).此表中ail=aii=i,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.

(1)写出数表的第六行(从左至右依次列出).
(2)设第n行的第二个数为bn(n≥2),求bn.
(3)令![]() ,记Tn为数列
,记Tn为数列![]() 前n项和,求
前n项和,求![]() 的最大值,并求此时n的值.
的最大值,并求此时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下面四个命题,其中正确命题的序号是( )
①“直线![]() 、
、![]() 不相交”是“直线
不相交”是“直线![]() 、
、![]() 为异面直线”的充分而不必要条件;②“直线
为异面直线”的充分而不必要条件;②“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() 平面
平面![]() ”;③“直线
”;③“直线![]() 直线
直线![]() ”的充要条件是“
”的充要条件是“![]() 平行于
平行于![]() 所在的平面”;④“直线
所在的平面”;④“直线![]() 平面
平面![]() ”的必要而不充分条件是“直线
”的必要而不充分条件是“直线![]() 平行于
平行于![]() 内的一条直线.”
内的一条直线.”
A.①③B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
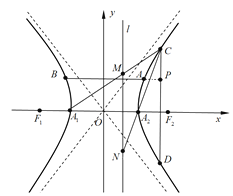
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 是实数常数)的图像上的一个最高点是
是实数常数)的图像上的一个最高点是![]() ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是![]() .
.
(1)求函数![]() 的解析式及其单调递增区间;
的解析式及其单调递增区间;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() ,角
,角![]() 的取值范围是区间
的取值范围是区间![]() 。当
。当![]() 时,试求函数
时,试求函数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫、精准脱贫”的号召,某贫困县在精准推进上下实功,在在精准落实上见实效现从全县扶贫对象中随机抽取![]() 人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分
人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分![]() 分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于
分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于![]() 分)和“很满意”(分数不低于
分)和“很满意”(分数不低于![]() 分)三个级别.
分)三个级别.

(1)求茎叶图中数据的平均数和![]() 的值;
的值;
(2)从“满意”和“很满意”的人中随机抽取![]() 人,求至少有
人,求至少有![]() 人是“很满意”的概率.
人是“很满意”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在常数M,使得对任意
,若存在常数M,使得对任意![]() ,
,![]() 与
与![]() 中至少有一个不小于M,则记作
中至少有一个不小于M,则记作![]() ,那么下列命题正确的是( ).
,那么下列命题正确的是( ).
A.若![]() ,则数列
,则数列![]() 各项均大于或等于M;
各项均大于或等于M;
B.若![]() ,则
,则![]() ;
;
C.若![]() ,
,![]() ,则
,则![]() ;
;
D.若![]() ,则
,则![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,青蒿素作为一线抗疟药品得到大力推广某农科所为了深入研究海拔因素对青蒿素产量的影响,在山上和山下的试验田中分别种植了![]() 株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了
株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了![]() 株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
编号位置 | ① | ② | ③ | ④ |
山上 |
|
|
|
|
山下 |
|
|
|
|
(1)根据样本数据,试估计山下试验田青蒿素的总产量;
(2)记山上与山下两块试验田单株青蒿素产量的方差分别为![]() ,
,![]() ,根据样本数据,试估计
,根据样本数据,试估计![]() 与
与![]() 的大小关系(只需写出结论);
的大小关系(只需写出结论);
(3)从样本中的山上与山下青蒿中各随机选取![]() 株,记这
株,记这![]() 株的产量总和为
株的产量总和为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com