
已知 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2) 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有 .
.
见解析
【解析】
试题分析:(1)正确.在等差数列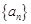 中,
中,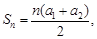 则
则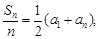 这表明点
这表明点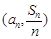 的坐标适合方程
的坐标适合方程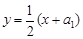 ,于是点
,于是点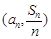 均在直线
均在直线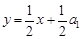 上.
上.
(2)正确.设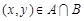 ,则(x,y)中的坐标x,y应是方程组
,则(x,y)中的坐标x,y应是方程组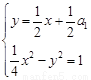 的解.由方程组消去y得:
的解.由方程组消去y得: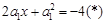 ,当a1=0时,方程(*)无解,此时
,当a1=0时,方程(*)无解,此时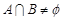 ;当a1≠0时,方程(*)只有一个解
;当a1≠0时,方程(*)只有一个解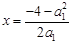 ,此时,方程组也只有一个解
,此时,方程组也只有一个解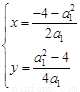 ,故上述方程组至多有一解.
,故上述方程组至多有一解.
∴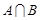 至多有一个元素.
至多有一个元素.
(3)不正确.取a1=1,d=1,对一切的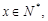 有
有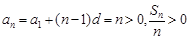 ,这时
,这时 集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于
集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于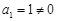 .如果
.如果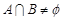 ,那么由(2)知
,那么由(2)知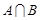 中至多有一个元素
中至多有一个元素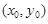 ,而
,而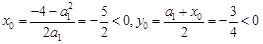 ,
,
这样的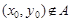 ,矛盾,故a1=1,d=1时
,矛盾,故a1=1,d=1时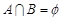 ,所以a1≠0时,一定有
,所以a1≠0时,一定有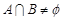 是不正确的.
是不正确的.
考点:本题主要考查集合的运算、等差数列及其性质、直线方程。
点评:这是解析几何与数列的综合题目,属中档题。对于数列的应用考查的比较多,这种题目可以作为高考卷的压轴题目出现,题目中对于最后一问的证明要注意应用前面的结论。


科目:高中数学 来源: 题型:
| Sn |
| n |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-1 1.1命题及其关系练习卷(解析版) 题型:解答题
已知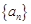 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合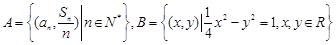 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)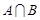 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有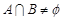 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com