已知a1=3且an=Sn-1+2n,则an= ;Sn= .
【答案】分析:由a1=3,an=Sn-1+2n,知an-an-1=(Sn-1+2n)-(Sn-2+2n-1)=an-1+2n-1,所以an=2an-1+2n-1,an+1=2(an+2n)=2(2an-1+2n-1)+2n=22an-1+2×2n=22(2an-2+2n-2)+2×2n=23an-2+3×2n=…=2n•a1+n×2n=(n+3)×2n,由此能求出an和Sn.
解答:解:∵a1=3,an=Sn-1+2n,
∴an-an-1=(Sn-1+2n)-(Sn-2+2n-1)
=an-1+2n-1,
即an=2an-1+2n-1,
an+1=2(an+2n)=2(2an-1+2n-1)+2n
=22an-1+2×2n
=22(2an-2+2n-2)+2×2n
=23an-2+3×2n
=…
=2n•a1+n×2n
=(n+3)×2n,
∴an=(n+2)×2n-1.
∵an=Sn-1+2n,
∴Sn=an+1-2n+1
=(n+3)×2n-2n+1
=(n+1)×2n.
故答案为:(n+2)×2n-1,(n+1)×2n.
点评:本题考查数列的综合应用,解题时要认真审题,仔细解答,注意递推公式的合理运用.



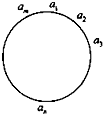 如图所示:m个实a1a2…,am(m≥3且m∈N)依次按顺时针方向围成一个圆圈.
如图所示:m个实a1a2…,am(m≥3且m∈N)依次按顺时针方向围成一个圆圈.