
(本小题共14分)
某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、
B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如下表:
 如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
科目:高中数学 来源: 题型:
(本小题共14分)
如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() ,点E在棱PB上。
,点E在棱PB上。

(Ⅰ)求证:平面![]() ;
;
(Ⅱ)当![]() 且E为PB的中点时,求AE与平面PDB所成的角的大小。
且E为PB的中点时,求AE与平面PDB所成的角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009北京理)(本小题共14分)
已知双曲线![]() 的离心率为
的离心率为![]() ,右准线方程为
,右准线方程为![]()
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 是圆
是圆![]() 上动点
上动点![]() 处的切线,
处的切线,![]() 与双曲线
与双曲线![]() 交
交
于不同的两点![]() ,证明
,证明![]() 的大小为定值.
的大小为定值.
查看答案和解析>>
科目:高中数学 来源:2013届度广东省高二上学期11月月考理科数学试卷 题型:解答题
(本小题共14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF PB交PB于点F
PB交PB于点F
⑴求证:PA//平面EDB
⑵求证:PB 平面EFD
平面EFD
⑶求二面角C-PB-D的大小

查看答案和解析>>
科目:高中数学 来源:2010年北京市崇文区高三下学期二模数学(文)试题 题型:解答题
(本小题共14分)
正方体 的棱长为
的棱长为 ,
, 是
是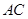 与
与 的交点,
的交点, 为
为 的中点.
的中点.
(Ⅰ)求证:直线 ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com