
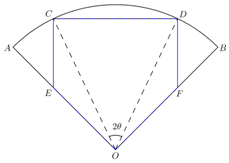
 现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.
现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.分析 (1)设M是CD中点,连OM,推出∠COM=∠DOM=$\frac{1}{2}∠COD=θ$,MD=Rsinθ,利用△CEO≌△DFO,转化求解∠DFO=$\frac{3π}{4}$,在△DFO中,利用正弦定理$\frac{DF}{sin∠DOF}=\frac{DO}{sin∠DFO}$,求解S=S△COD+SODF+SOCE=S△COD+2SODF的解析式即可.
(2)利用S的解析式,通过三角函数的最值求解即可.
解答 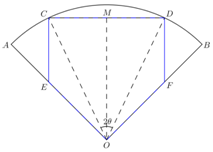 解:(1)设M是CD中点,连OM,由OC=OD,可知OM⊥CD,
解:(1)设M是CD中点,连OM,由OC=OD,可知OM⊥CD,
∠COM=∠DOM=,$\frac{1}{2}∠COD=θ$,MD=Rsinθ,
又OE=OF,EC=FD,OC=OD,可得△CEO≌△DFO,
故∠EOC=∠DOF,可知$∠AOM=∠BOM=\frac{1}{2}∠AOB=\frac{π}{4}$,…(2分)
又DF⊥CD,OM⊥CD,所以MO∥DF,故∠DFO=$\frac{3π}{4}$,
在△DFO中,有$\frac{DF}{sin∠DOF}=\frac{DO}{sin∠DFO}$,
可得$DF=\frac{{Rsin(\frac{π}{4}-θ)}}{{sin\frac{3π}{4}}}=R(cosθ-sinθ)$…(5分)
所以S=S△COD+SODF+SOCE=S△COD+2SODF=$\frac{1}{2}{R^2}sin2θ+Rsinθ(Rcosθ-Rsinθ)$
=${R^2}sin2θ-{R^2}{sin^2}θ(0<θ<\frac{π}{4})$…(8分)
(2)$S={R^2}sin2θ-\frac{1}{2}{R^2}(1-cos2θ)={R^2}(sin2θ+\frac{1}{2}cos2θ)-\frac{1}{2}{R^2}$…(10分)
=$\frac{{\sqrt{5}}}{2}{R^2}sin(2θ+φ)-\frac{1}{2}{R^2}$(其中$φ=arctan\frac{1}{2}$) …(12分)
当$2θ+φ=\frac{π}{2}$,即$θ=\frac{π}{4}-\frac{φ}{2}$时,sin(2θ+φ)取最大值1.
又$\frac{π}{4}-\frac{φ}{2}$$∈(0,\frac{π}{4})$,所以S的最大值为$\frac{{\sqrt{5}-1}}{2}{R^2}$. …(14分)
点评 本题考查函数与方程的实际应用,三角函数的最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
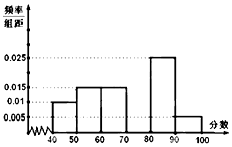 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 7 | C. | 5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com