
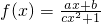 (a,b,c为常数,a≠0).
(a,b,c为常数,a≠0).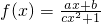 的图象上,求an的前n项和Sn;
的图象上,求an的前n项和Sn;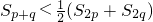 ;
;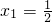 ,xn+1=f(xn),求证:
,xn+1=f(xn),求证: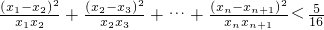 .
.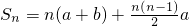 =
=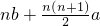 .
.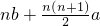 .(2分)
.(2分)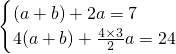 即
即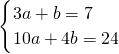 解得
解得
 .(3分)
.(3分)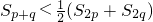 .(5分)
.(5分)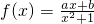 .
.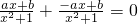 .解得b=0.所以
.解得b=0.所以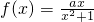 .
.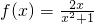 .(6分)
.(6分)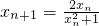 .所以
.所以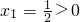 时,有xn+1>0(n∈N*).
时,有xn+1>0(n∈N*). ,
,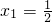 矛盾.
矛盾.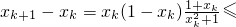
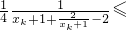
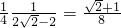 .
.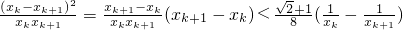 .(10分)
.(10分)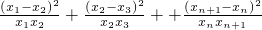
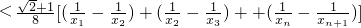 =
=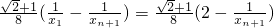 .(12分)
.(12分)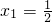 ,xn+1>xn,所以
,xn+1>xn,所以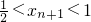 .所以
.所以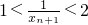 .
.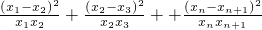
 .(14分)
.(14分)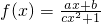 ,因为点(n,an)在函数f(x)=ax+b的图象上,可得an是首项是a1=a+b,公差为d=a的等差数列,从而求出an的前n项和Sn;
,因为点(n,an)在函数f(x)=ax+b的图象上,可得an是首项是a1=a+b,公差为d=a的等差数列,从而求出an的前n项和Sn;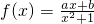 .因为f(x)为奇函数,所以f(-x)+f(x)=0,代入求出b值,从而求出f(x)的表达式,然后利用放缩法进行证明;
.因为f(x)为奇函数,所以f(-x)+f(x)=0,代入求出b值,从而求出f(x)的表达式,然后利用放缩法进行证明;

科目:高中数学 来源:2011年四川省内江六中高考数学模拟试卷(文科)(解析版) 题型:解答题
 (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,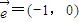 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com