已知数列a,b,c是各项均为正数的等差数列,公差为d(d>0).在a,b之间和b,c之间共插入n个实数,使得这n+3个数构成等比数列,其公比为q.
(1)求证:|q|>1;
(2)若a=1,n=1,求d的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且s,t都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用a,c,n表示).
【答案】
分析:(1)先由条件求出知
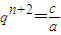
,又有c=a+2d代入即可得|q
n+2|>1,就可证明结论;
(2)先求出b=1+d,c=1+2d,然后对插入的数分所在位置所存在的两种情况分别求出d的值即可;
(3)先由条件求得|q|
s+1>|q|
t+1⇒s>t.然后再对q所存在的可为正数,也可为负数两种情况分别求出插入的n个数的乘积即可.
解答:解:(1)由题意知
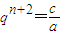
,c=a+2d,
又a>0,d>0,可得
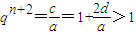
,(2分)
即|q
n+2|>1,故|q|
n+2>1,又n+2是正数,故|q|>1.(4分)
(2)由a,b,c是首项为1、公差为d的等差数列,故b=1+d,c=1+2d,
若插入的这一个数位于a,b之间,则1+d=q
2,1+2d=q
3,
消去q可得(1+2d)
2=(1+d)
3,即d
3-d
2-d=0,其正根为
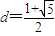
.(7分)
若插入的这一个数位于b,c之间,则1+d=q,1+2d=q
3,
消去q可得1+2d=(1+d)
3,即d
3+3d
2+d=0,此方程无正根.
故所求公差
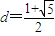
. (9分)
(3)由题意得
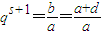
,
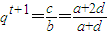
,又a>0,d>0,
故
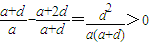
,可得

,又
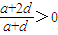
,
故q
s+1>q
t+1>0,即|q|
s+1>|q|
t+1.
又|q|>1,故有s+1>t+1,即s>t. (12分)
设n+3个数所构成的等比数列为a
n,则
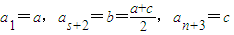
,
由a
ka
n+4-k=a
1a
n+3=ac(k=2,3,4,n+2),
可得(a
2a
3a
n+2)
2=(a
2a
n+2)(a
3a
n+1)(a
n+1a
3)(a
n+2a
2)=(ac)
n+1,(14分)
又
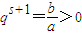
,
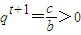
,
由s,t都为奇数,则q既可为正数,也可为负数,
①若q为正数,则a
2a
3a
n+2=
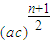
,插入n个数的乘积为
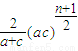
;
②若q为负数,a
2,a
3,a
n+2中共有
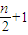
个负数,
故a
2a
3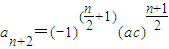
,所插入的数的乘积为
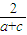
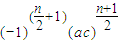
.
所以当n=4k-2(k∈N
*)时,所插入n个数的积为
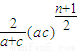
;
当n=4k(k∈N
*)时,所插入n个数的积为
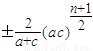
.(18分)
点评:本题综合考查等差数列与等比数列的基础知识以及分类讨论思想在解题中的应用.本题的前二问比较基础,第三问比较麻烦,适合程度较高的学生解答.

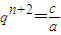 ,又有c=a+2d代入即可得|qn+2|>1,就可证明结论;
,又有c=a+2d代入即可得|qn+2|>1,就可证明结论;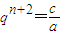 ,c=a+2d,
,c=a+2d,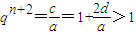 ,(2分)
,(2分)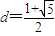 .(7分)
.(7分)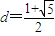 . (9分)
. (9分)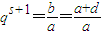 ,
,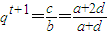 ,又a>0,d>0,
,又a>0,d>0,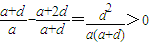 ,可得
,可得 ,又
,又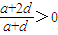 ,
,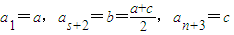 ,
,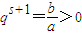 ,
,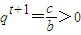 ,
,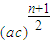 ,插入n个数的乘积为
,插入n个数的乘积为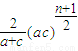 ;
;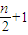 个负数,
个负数,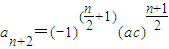 ,所插入的数的乘积为
,所插入的数的乘积为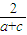
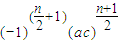 .
.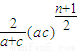 ;
;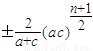 .(18分)
.(18分)

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案