
在空间中,取直线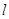 为轴,直线
为轴,直线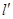 与
与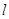 相交于点
相交于点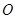 ,其夹角为
,其夹角为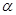 (
(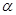 为锐角),
为锐角),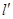 围绕
围绕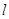 旋转得到以
旋转得到以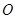 为顶点,
为顶点,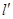 为母线的圆锥面,任取平面
为母线的圆锥面,任取平面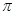 ,若它与轴
,若它与轴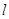 交角为
交角为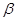 (
(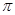 与
与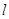 平行时,记
平行时,记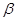 =0),则:当
=0),则:当 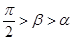 时,平面
时,平面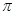 与圆锥面的交线为 .
与圆锥面的交线为 .
科目:高中数学 来源: 题型:
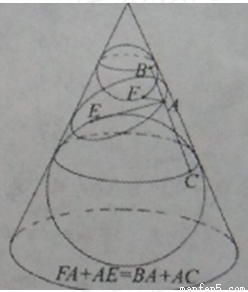
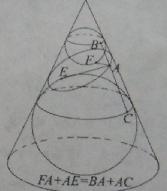
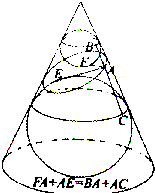 在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当
在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当 | π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)β>α, __________________________;
(2)β=α, __________________________;
(3)β<α, __________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
在空间中,取直线![]() 为轴,直线
为轴,直线![]() 与
与![]() 相交于点
相交于点![]() ,其夹角为
,其夹角为![]() (
(![]() 为锐角),
为锐角),![]() 围绕
围绕![]() 旋转得到以
旋转得到以![]() 为顶点,
为顶点,![]() 为母线的圆锥面,任取平面
为母线的圆锥面,任取平面![]() ,若它与轴
,若它与轴![]() 交角为
交角为![]() (
(![]() 与
与![]() 平行时,记
平行时,记![]() =0),则:当
=0),则:当 ![]() 时,平面
时,平面![]() 与圆锥面的交线为 .
与圆锥面的交线为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com