一个袋子中装有不同颜色的6个小球,其中标有数字1、2、3的小球各2个,这些小球无其他区别,现从袋子中任取3个小球.
(I)求取出的3个小球中恰有2个数字相同的概率;
(Ⅱ)设取出的3个小球上的数字之和为ξ,求ξ的分布列和期望.
分析:(I)“取出的3个小球中恰有2个数字相同”的对立事件为“取出的三个小球的数字均不相同”,利用古典概型和对立事件的概率求解即可;
(Ⅱ)取出的三个小球的数字可能为(1,1,2)、(1,1,3)、(1,2,2)、(1,2,3)、(2,2,3)、(2,3,3)
故ξ的所有可能取值为4,5,6,7,8,用古典概型分别求概率,列出分布列,再求期望即可.
解答:解:(I)记“取出的3个小球中恰有2个数字相同”为事件A,则A的对立事件为:“取出的三个小球的数字均不相同”,
所以P(A)=1-
=(Ⅱ)ξ的所有可能取值为4,5,6,7,8,
ξ=4仅一类(1,1,2),p(ξ=4)=
=ξ=5有两类(1,1,3)、(1,2,2),p(ξ=5)=
=ξ=6有一类(1,2,3)p(ξ=6)=
=
ξ=7有两类(2,2,3)、(1,3,3)p(ξ=7)=
=
ξ=8有一类(2,3,3)p(ξ=8)=
=
所以Eξ=6
点评:本题考查对立事件、互斥事件的概率、离散型随机变量的分布列和期望等知识,考查利用所学知识解决问题的能力.



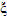 ,求
,求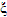 的分布列和期望.
的分布列和期望.