Question

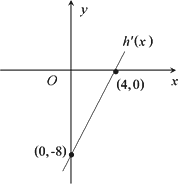
已知二次函数h(x)＝ax²＋bx＋c(c>0)，其导函数y＝h′(x)的图象如下，且f(x)＝ln x－h(x)．

(1)求函数f(x)在x＝1处的切线斜率；

(2)若函数f(x)在上是单调函数，求实数m的取值范围；

(3)若函数y＝2x－lnx(x∈[1,4])的图象总在函数y＝f(x)的图象的上方，求c的取值范围．

 

Answer 1

【答案】

(1)由题知，h′(x)＝2ax＋b，其图象为直线，且过A(2，－1)、B(0,3)两点，

∴，解得. zxxk

∴h(x)＝－x²＋3x＋c.

∴f(x)＝ln x－(－x²＋3x＋c)＝x²－3x－c＋ln x.

∴f′(x)＝2x－3＋，

∴f′(1)＝2－3＋＝0，

所以函数f(x)在x＝1处的切线斜率为0.

(2)由题意可知，函数f(x)的定义域为(0，＋∞)，zxxk

由(1)知，f′(x)＝2x－3＋＝＝.

令f′(x)＝0，得x＝或x＝1.

当x变化时，f(x)、f′(x)随x的变化情况如下表：

x				1	(1，＋∞)
f′(x)	＋	0	－	0	＋
f(x)	?	极大值	?	极小值	?

∴f(x)的单调递增区间为，(1，＋∞)．

f(x)的单调递减区间为.

要使函数f(x)在区间上是单调函数，

则，解得<m≤.

故实数m的取值范围是.

(3)由题意可知，2x－ln x>x²－3x－c＋ln x在x∈[1,4]上恒成立，

即当x∈[1,4]时，c>x²－5x＋2ln x恒成立

设g(x)＝x²－5x＋2ln x，x∈[1,4]，则c>g(x)_max.

易知g′(x)＝2x－5＋＝＝.

令g′(x)＝0得，x＝或x＝2. zxxk

当x∈(1,2)时，g′(x)<0，函数g(x)单调递减；当x∈(2,4)时，g′(x)>0，函数g(x)单调递增．

而g(1)＝1²－5×1＋2ln 1＝－4，g(4)＝4²－5×4＋2ln 4＝－4＋4ln 2，

显然g(1)<g(4)，故函数g(x)在[1,4]上的最大值为g(4)＝－4＋4ln 2，

故c>－4＋4ln 2.

∴c的取值范围为(－4＋4ln 2，＋∞)

【解析】略