
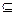 [1,4],求实数a的取值范围?
[1,4],求实数a的取值范围?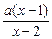 >1(a≠1)。
>1(a≠1)。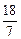 )(2)当a>1时解集为(-∞,
)(2)当a>1时解集为(-∞,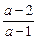 )∪(2,+∞);当0<a<1时,解集为(2,
)∪(2,+∞);当0<a<1时,解集为(2,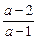 );当a=0时,解集为
);当a=0时,解集为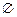 ;当a<0时,解集为(
;当a<0时,解集为(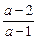 ,2)。
,2)。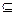 [1,4]有两种情况:其一是M=
[1,4]有两种情况:其一是M=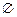 ,此时Δ<0;其二是M≠
,此时Δ<0;其二是M≠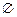 ,此时Δ=0或Δ>0,分三种情况计算a的取值范围
,此时Δ=0或Δ>0,分三种情况计算a的取值范围
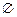
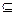 [1,4];
[1,4];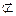 [1,4];当a=2时,m={2}
[1,4];当a=2时,m={2}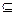 [1,4]。
[1,4]。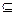 [1,4]
[1,4]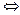 1≤x1<x2≤4
1≤x1<x2≤4 ,
,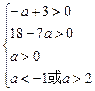 ,解得2<a<
,解得2<a<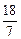 ,
,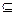 [1,4]时,a的取值范围是(-1,
[1,4]时,a的取值范围是(-1,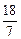 )。
)。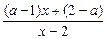 >0,
>0,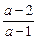 )(x-2)>0同解。
)(x-2)>0同解。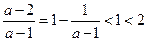 ,
,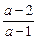 )∪(2,+∞)。
)∪(2,+∞)。 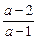 )(x-2) <0同解。
)(x-2) <0同解。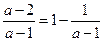 ,
,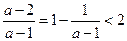 ,解集为(
,解集为(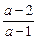 ,2);
,2);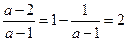 ,解集为
,解集为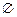 ;
;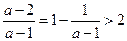 ,解集为(2,
,解集为(2,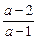 )。
)。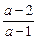 )∪(2,+∞);当0<a<1时,解集为(2,
)∪(2,+∞);当0<a<1时,解集为(2,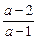 );当a=0时,解集为
);当a=0时,解集为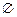 ;当a<0时,解集为(
;当a<0时,解集为(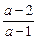 ,2)。
,2)。

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
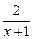 >2的解集是
>2的解集是| A.(-1,0)∪(1,+∞) | B.(-∞,-1)∪(0,1) |
| C.(-1,0)∪(0,1) | D.(-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| ax+b |
| (k+1)x-k |
| 2-x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com